mymachine
- 42
- 0
Hi everyone,
I would like to ask about the continuity of the cubic Bezier curve.
There are two cubic Bezier curves, A and B, shown as below two images:
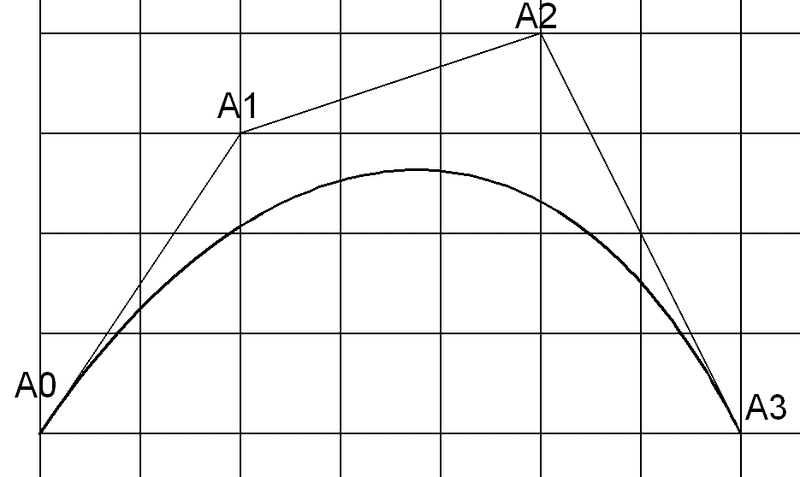
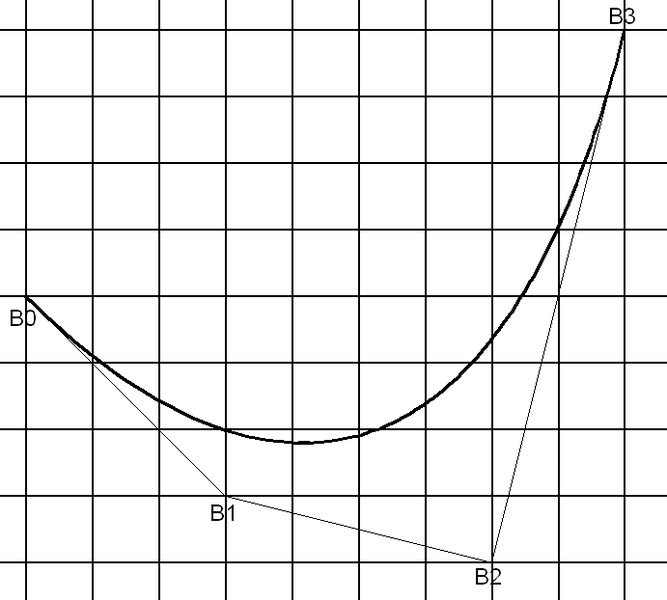
The coordinates of the A curve are:
A0 = (x0,y0) = (0,0)
A1 = (x1,y1) = (2,3)
A2 = (x2,Y2) = (5,4)
A3 = (x3,y3) = (7,0)
The coordinates of the B curve are:
B0 = (x0,y0) = (0,4)
B1 = (x1,y1) = (3,1)
B2 = (x2,y2) = (7,0)
B3 = (x3,y3) = (9,8)
If I join these two curves together by connecting the point A3 and B0, it looks such as below image:
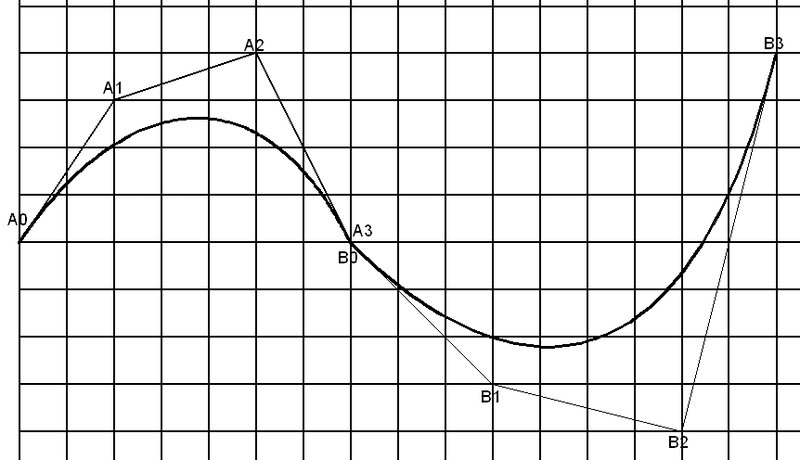
However, the curve doesn't looks smooth at point A3 = B0.
The question is, what is the equation of the Bezier curve start from
point A0 > A1 > A2 > A3=B0 > B1 > B2 > B3
where the endpoint is A0, A3 = B0, and B3
and so that the curve is continue and looks smooth?
Also, does this A+B curve is 7th degree of the Bernstein polynomial?
Thank you
I would like to ask about the continuity of the cubic Bezier curve.
There are two cubic Bezier curves, A and B, shown as below two images:
The coordinates of the A curve are:
A0 = (x0,y0) = (0,0)
A1 = (x1,y1) = (2,3)
A2 = (x2,Y2) = (5,4)
A3 = (x3,y3) = (7,0)
The coordinates of the B curve are:
B0 = (x0,y0) = (0,4)
B1 = (x1,y1) = (3,1)
B2 = (x2,y2) = (7,0)
B3 = (x3,y3) = (9,8)
If I join these two curves together by connecting the point A3 and B0, it looks such as below image:
However, the curve doesn't looks smooth at point A3 = B0.
The question is, what is the equation of the Bezier curve start from
point A0 > A1 > A2 > A3=B0 > B1 > B2 > B3
where the endpoint is A0, A3 = B0, and B3
and so that the curve is continue and looks smooth?
Also, does this A+B curve is 7th degree of the Bernstein polynomial?
Thank you