How will a capacitor influence a lightbulb?

[Dart82]

Homework Statement

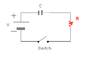
Consider the simple circuit shown below, in which a light bulb with resistance R and a capacitor with capacitance C are connected in series with a battery and an open switch. The capacitor has a large capacitance and is initially uncharged. The battery provides enough power to light the bulb when it is connected directly to the battery. What happens when the switch is closed?

[URL=http://imageshack.us][PLAIN]http://img169.imageshack.us/img169/229/question7lg1.gif[/URL][/PLAIN]


A) Nothing
B) The light bulb glows with a constant intensity.
C) The light bulb gradually gets brighter as time passes.
D) The light bulb starts out at its brightest and then gradually gets
dimmer as time passes. [my second guess]
E) The light bulb blinks on and off. [my 1st guess]

Homework Equations

no equation necessary

The Attempt at a Solution

My 1st thoughts:
Well i thought that the current would flow from the battery to the capacitor, where it would be stored. When the capacitor discharged it would send the current through the lightbulb, causing it to flash on and off.

Apparently this is faulty thinking, as E is not the correct answer.

my second thoughts: electrons flow from regions of low potential, such as those found on a - battery terminal to regions of higher potential. Therefore, the electrons will "flow" from the negative battery terminal across the closed switch and through the filament of the lightbulb, thus illuminating it. Next, the electrons will flow into the capacitor where they will be stored. As the capacitor's stored charge builds, it "sucks" more and more available current from the lightbulb, causing it to dim.

Feel free to poke any holes in my theory.

 

[turdferguson]

Youre second guess is correct. A capacitor will not discharge itself unless the battery is taken out of the circuit and a complete closed path remains. Take a look at figure 3 in this link: http://phoenix.phys.clemson.edu/labs/223/rc/index.html

As your capacitor charges, it will gain more voltage and the current in the circuit will decrease to zero

 

[Dart82]

Thanks for the help!

 

[andrevdh]

When the switch is closed the current can flow in the circuit since the capacitor "absorbs" it. The bulb will therefore glow, but as the charge accumulates on the plates of the capacitor a voltage builds up over it. This voltage opposes that of the battery. The current in the circuit will then decrease as the voltage builds up over the capacitor and eventually stop when the capacitor is charged up to the same voltage as the battery. A charged capacitor acts like a battery, but its voltage drops as it discharges.