The relation between angular and linear momentum

[Cleonis]

In the image above the line ABCDE represents the trajectory of a point mass, in inertial motion. Point S is in inertial motion also. As we know, in inertial motion equal distances are covered in equal intervals of time.

All of the consecutive triangles (SAB, SBC, etc) have the same area, as they have the same base and same height. This implies that equal areas are swept out in equal intervals of time.


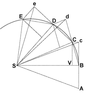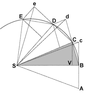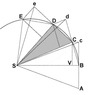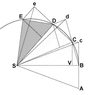
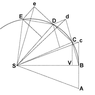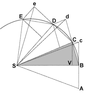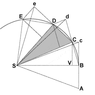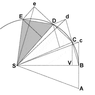
The image below reproduces Newton's demonstration that Kepler's law of areas follows from the laws of motion.

A point mass is traveling along the curvilinear trajectory BCDE
Point S represents the common center of mass of two point masses that attract each other. It follows from the third law that point S is in inertial motion. The force upon the traveling point mass is at all times towards point S.

Without any force the point mass would proceed to point c. At point B the point mass receives an impulse towards S. The resulting motion is the vector sum of the original velocity and the added velocity component. This algorithm is repeated over the length of the curve.

The consecutive triangles all have the same area. In the limit of infinitisimal time increments the segments produce the curve.


I think these geometric demonstrations illustrate that angular momentum is a compound entity, reducible to elements. The elements of angular momentum are Newton's laws of motion.

 

[mordechai9]

Cleonis, I replied in the other thread because the OP in this post seems a little bit different from what we were talking about there. You may be correct that our disagreement is just about definitions. Anyways --

I agree with you about the interpretation of the angular momentum laws as theorems. That is a nice way of putting it. However, force laws being an axiom and angular momentum laws being theorems does not imply they are dependent, mathematically speaking. For example, you wouldn't say calculus is really dependent on the axioms of set theory. In most cases in calculus, you don't care at all about set theory, even though strictly speaking they are obviously dependent.

What I really meant was that angular momentum and linear momentum are linearly independent, in the sense that $$( r \times (mv) ) \cdot (mv) = 0$$.

 

[LostConjugate]

What I really meant was that angular momentum and linear momentum are linearly independent, in the sense that $$( r \times (mv) ) \cdot (mv) = 0$$.

Isn't it the definitions that are linearly independent? The cross product gives us the norm to an imaginary surface where v is the actual path of a massive particle.

 

[Cleonis]

I agree with you about the interpretation of the angular momentum laws as theorems. That is a nice way of putting it. However, force laws being an axiom and angular momentum laws being theorems does not imply they are dependent, mathematically speaking. For example, you wouldn't say calculus is really dependent on the axioms of set theory. In most cases in calculus, you don't care at all about set theory, even though strictly speaking they are obviously dependent.

What I really meant was that angular momentum and linear momentum are linearly independent, in the sense that $$( r \times (mv) ) \cdot (mv) = 0$$.

OK, we agree as to the status of angular momentum as a theorem of the laws of motion.

For completeness: when I refer to laws of motion I think of a modernized formulation of them. This modernized formulation is designed to be logically equivalent with the traditional formulation, but more suited to the purpose.

1. When an object is in inertial motion it covers equal distances in equal intervals of time (This law asserts uniformity of space and time.)
2. F=m*a (to define the concept of force)
3. When two objects interact (attracting or repelling each other) then their common center of mass remains in inertial motion. (Once again asserting uniformity of space and time.)

(This version of the 3rd law is exclusively about dynamics. Newton's formulation of the 3rd law attempts so cover statics also, which is a superfluous attempt.)



(Pressed for time now, I'll post some more comment tomorrow.)

 

[Cleonis]

I agree with you about the interpretation of the angular momentum laws as theorems. That is a nice way of putting it. However, force laws being an axiom and angular momentum laws being theorems does not imply they are dependent, mathematically speaking. For example, you wouldn't say calculus is really dependent on the axioms of set theory. In most cases in calculus, you don't care at all about set theory, even though strictly speaking they are obviously dependent.

What I really meant was that angular momentum and linear momentum are linearly independent, in the sense that $$( r \times (mv) ) \cdot (mv) = 0$$.

I'd like to take a closer look at the comparison with calculus. The first post of this thread presents a diagram that shows Newton's derivation of Kepler's second law. Newton uses a precursor of differential calculus. His derivation rests on taking the limit of infinitisimal time increments. Whereas Newton had to take the limit explicitly in all his proofs, today we can expect everyone to be familiar with differential calculus, allowing more complicated problems to be addressed.

(Yet another comparison: levels of computer language. The very first computers were programmed in machine language, then assembler languages were developed, then third generation languages. Each language level is dependent on services rendered by the level below it. Using the higher level environment is much more efficient use of programmer man-hours.)

In physics computations angular momentum is used in situation where it gives an efficiency advantage. Still, if a phenomenon can be accounted for in terms of angular momentum it can also be accounted for in terms of instantaneous linear momentum of two or more interacting objects. This is always valid, since angular momentum is reducible, with the laws of motion as elements.


In physics I distinguish between what matters for efficiency advantage and what matters for understanding at gut level. What is best for computational efficiency is not necessarily suitable for gut level understanding.

In the case of gyroscopic precession the computation that uses the angular momentum of the spinning top and the vector cross product you readily get the correct prediction of the motion, but it doesn't illuminate why the spinning top tends to precess.

Interestingly, understanding why the vector cross product arises in the first place is in fact accessible. That is https://www.physicsforums.com/showpost.php?p=2697666&postcount=3" in the thread about how a rolling hoops remain upright.