Applying Kirchoff's Law to a Short-Circuited Resistor: Where Is the Fallacy?

[saubhik]

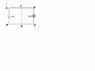
In the attachment (also given at bottom for your convenience) you can see the circuit diagram. We all know that the 5 ohm resistor is short-circuited so no current flows through the resistor. But if we apply Kirchoff's loop law with the following symbols:

i = current through DBAC from positive terminal of battery
i1 = current through CD from junction C
i-i1 = current through CEFD from E​

we get,
from loop AEFBA,

5(i-i1) = 5 or i-i1 = 1​

from loop CEFDC,

5(i-i1) = 0 or i-i1 = 0​

Thus ambiguity arises.
Can anyone please explain me where I am going wrong ?

Also if we apply loop law to BDCAB,

5 = 0​

Where is the fallacy here? (i mean, where am i wrong ? )

Thank you.

[PLAIN]http://img594.imageshack.us/img594/7609/circuit.jpg

 

[tiny-tim]

Hi saubhik!

Your diagram assumes that DBAC and CD both have zero resistance.

I think if you put in an actual small resistance (say 10^-6), then everything will be ok.

 

[saubhik]

Thnx tiny-tim for the fast reply
But assuming that DBAC and CD both have zero resistance, can't we apply Kirchoff's laws. (in fact that's what we do in our regular exercises?)
So, you mean kirchhoffs laws not applicable for ideal situations?

 

[tiny-tim]

So, you mean kirchhoffs laws not applicable for ideal situations?

uhhh? what's ideal about zero resistance and infinite current?

No, you can't apply Kirchhoff (two h's ) if any part of the circuit would have infinite current.

 

[saubhik]

can anyone tell me about the origin of loop law or may be its proof?

 

[saubhik]

uhhh? what's ideal about zero resistance and infinite current?

I kind of meant "abstract" situations referring to zero resistance and infinite current
By physical reasonings can you prove the loop law?

 

[tiny-tim]

Work done = charge times potential difference.

So the total potential difference round a loop has to equal zero (if it didn't, you could move a charge all the way round the circuit and extract work ).

And potential difference for a resistance happens to be IR (there are diffferent formulas for other devices).

 

[Studiot]

Where is the fallacy here? (i mean, where am i wrong ? )

The fallacy is that you are not applying Kirchoffs voltage law correctly. When two points are at the same potential because they are connected by a wire (short ) they are the same point for the purposes of KVL.

If you look at you diagram Points A, B, C, D, E and F are all connected by a wire or short and are therefore at the same potential and are therefore part of the same point. This is no different form a point midway between say C and E which can be considered as part of C or E.

Since all points are really pat of one large 'superpoint' you do not have even one loop to apply KVL to.

What this is telling you is that by introducing the short you have the same situation as if you had one terminal only and connected both ends of your resistor and battery to it.

 

[vaibhav1803]

can anyone tell me about the origin of loop law or may be its proof?

i beg to disagree with tiny tim,loop law is for the ideal situation(what u n i hav learnt),
so if u want to prove it rigorously, no I am not giving full solutions(it'll kill me) to you conserve energy through different paths or more OBVIOUSLY start by saying that "a point in any circuit is at zero potential differnce with respect to itself thus extend this statement to a "loop" in the circuit(thats why you add up PD in any random order specifying that at the end of it its going to be zero, now try to get this on paper and see the "miracle happen"
hope i could help
vaibhav.

 

[vaibhav1803]

oh by the way if you haven't noticed PD across a pure conducter, saubhik is zero, hence the resistance is shorted out(PD across it also zero, if you try looking through it via current law) hencethe current through resistance is also ZERO.
problem solved..:P
can't believe everyone except 2 people here didnt notice that..:)

 

[saubhik]

i beg to disagree with tiny tim,loop law is for the ideal situation(what u n i hav learnt)

in case you are correct, then where am I wrong in my application of loop law on the above circuit diagram (in which i m getting ambiguous answers?)

 

[vaibhav1803]

in case you are correct, then where am I wrong in my application of loop law on the above circuit diagram (in which i m getting ambiguous answers?)

look one thread above yours I've posted 2 threads, one explanation one answer.