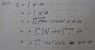- #1
Change of varibles in integrals (More than 1 question)
Click For Summary
The discussion centers on the challenges of integrating variables in spherical coordinates, specifically integrating θ from 0 to 2π and φ from 0 to π to generate a sphere. Participants highlight that the limits for θ integration are incorrect, as sin θ is positive for 0 < θ < π and negative for π < θ < 2π. Additionally, there are questions about integrating functions that involve both r and θ, with suggestions to use the substitution r = 2a cos(θ) to facilitate the integration. The density of the circular lamina is also discussed, defined as ρ = Mπa², where M represents mass per unit area. Clarifications on the limits of integration for θ are necessary for accurate results.
- #2
- #3
SammyS
Staff Emeritus
Science Advisor
Homework Helper
- 11,987
- 1,579
athrun200 said:
For 0 < θ < π sin θ is positive, for π < θ < 2π sin θ is negative.
- #4
SammyS
Staff Emeritus
Science Advisor
Homework Helper
- 11,987
- 1,579
For (d) : You have the wrong limits for the θ integration.athrun200 said:Homework Statement
I have questions on d and e
I don't know how to integrate these functions
Also, the density is given by ρ = M π a2, where M is the mass of the circular lamina and assumes that ρ is the mass per unit area.
For (e): Your integral has both r & θ in it.
I suggest using r = 2a cos (θ) to find dr/dθ . What are the limits of θ for this integral ?
Last edited:
Similar threads
- · Replies 9 ·
- · Replies 9 ·
- · Replies 3 ·
- · Replies 2 ·