What are the conditions for non-integer exponents to be single valued?

AI Thread Summary
Non-integer exponents can lead to multi-valued expressions, particularly in complex analysis. The discussion highlights the need for specific conditions under which these exponents can be treated as single-valued. It emphasizes that the initial equation presented is incorrect and suggests that there are no universal conditions that allow non-integer exponents to be single-valued. Further exploration in the field of complex functions may provide clarity on this issue. Understanding these principles is crucial for accurate mathematical modeling involving non-integer exponents.
Black Integra
Messages
56
Reaction score
0
Nothing much, I have this:
gif.latex?\dpi{150}%20e^\theta=(e^{i\theta})^{-i}=(e^{i(\theta+2\pi)})^{-i}=e^{\theta+2\pi}.gif


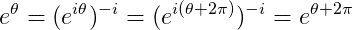
I have studied (myself) about this for many days.
And I believe that, for some conditions
gif.latex?\dpi{150}%20(e^\psi)^\phi\neq%20e^{\psi\phi}.gif
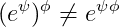for a complex ψ,ϕ

What are those conditions I mentioned about? And which field of study I should go to see?
 
Mathematics news on Phys.org
Your first equation is obviously wrong, as you can see. For the second question, there are no conditions where it doesn't hold.

The problem lies in the fact that for non-integer exponents, the expression is not single valued.
 
Thread 'Video on imaginary numbers and some queries'

Thread 'Video on imaginary numbers and some queries'

Hi, I was watching the following video. I found some points confusing. Could you please help me to understand the gaps? Thanks, in advance! Question 1: Around 4:22, the video says the following. So for those mathematicians, negative numbers didn't exist. You could subtract, that is find the difference between two positive quantities, but you couldn't have a negative answer or negative coefficients. Mathematicians were so averse to negative numbers that there was no single quadratic...
View full post »

Thread 'What Exactly is Dirac’s Delta Function? - Insight'

Insights auto threads is broken atm, so I'm manually creating these for new Insight articles. In Dirac’s Principles of Quantum Mechanics published in 1930 he introduced a “convenient notation” he referred to as a “delta function” which he treated as a continuum analog to the discrete Kronecker delta. The Kronecker delta is simply the indexed components of the identity operator in matrix algebra Source: https://www.physicsforums.com/insights/what-exactly-is-diracs-delta-function/ by...
View full post »
Thread 'Unit Circle Double Angle Derivations'

Thread 'Unit Circle Double Angle Derivations'

Here I made a terrible mistake of assuming this to be an equilateral triangle and set 2sinx=1 => x=pi/6. Although this did derive the double angle formulas it also led into a terrible mess trying to find all the combinations of sides. I must have been tired and just assumed 6x=180 and 2sinx=1. By that time, I was so mindset that I nearly scolded a person for even saying 90-x. I wonder if this is a case of biased observation that seeks to dis credit me like Jesus of Nazareth since in reality...
View full post »

Similar threads

Insights Views On Complex Numbers
3
Replies
108
Views
10K
I What Are Examples of Alternate Orderings in Mathematics?
Replies
2
Views
2K
B The Paradox of 1 – 1 + 1 – 1 + 1 – 1 + …
Replies
5
Views
2K
I Complex Analysis holomorphic condition
Replies
13
Views
2K
I Domain of single-valued logarithm of complex number z
Replies
2
Views
2K
B Are Inverse Problems More Complex Than Direct Problems in Mathematics?
Replies
13
Views
3K
A How Does U(1) Double-Cover SO(2) for a Specified Angle?
Replies
2
Views
2K
B How Does the Unit Circle Relate to Euler's Formula in Complex Numbers?
Replies
10
Views
3K
B Fractional/decimal powers
Replies
10
Views
2K
B Square root of a negative number in a complex field
Replies
45
Views
5K

Hot Threads

Recent Insights

Back
Top