JDoolin said:
There are some great things you can do with that dτ; in particular, setting it equal to zero, to see what the path of a photon through your curved space is. But that path is through the t, r, θ, and φ coordinates. Those coordinates are not meaningless. They are the overlying GLOBAL LORENTZ FRAME COORDINATES IN SPHERICAL FORM, COMOVING WITH THE CENTRAL MASS.
PeterDonis said:
If you really believe this, then please demonstrate how, in a curved spacetime with gravity present, two worldlines with the same constant θ and φ, and values of r that differ by a small amount dr, at a given instant of coordinate time t = 0, will continue to remain separated by that same amount dr for all times t. That is what is physically required for your global Lorentz frame coordinates to be valid. If this requirement is violated (which it is in the presence of gravity), your global Lorentz frame coordinates *will not work* the way you are claiming they do. You can *assign* such coordinates as arbitrary labels, but they will not support the claims about the physics that you appear to be making.
This is obvious. Surely you already know the answer I would give: Upon a non-rotating gravitating sphere, place one object on the floor at radius r. Place another object on a table directly above it at radius r+dr. The two objects will remain on the floor and on the table, maintaining their positions in r, theta, phi, but moving through time.
PeterDonis said:
There are at least two conceptual errors here. First, the metric, which you have written as a line element, is *not* a coordinate transformation equation. It is an equation that tells you how to calculate an actual physical interval along a differential segment of a curve in spacetime, if you know the coordinates and their differentials along that segment. If you integrate it along a worldline, it tells you the physical interval along that worldline; for example, along a timelike worldline, it tells you the proper time experienced by an observer following that worldline. But proper time is *not* a coordinate; it's a physical observable. The t, r, θ, and φ coordinates are *not* observables; they're arbitrary numbers that are used to label events.
In the Schwarzschild coordinates, theta, and phi are "arbitrary" in the following sense: Because the schwarzchild metric is spherically symmetric, you can choose the directions for θ=0 and φ=0 in any direction you like. The r coordinate is zero at the center of mass of the central gravitating body, so in that sense, r is not arbitrary. You might suggest that the scale of r is arbitrary since we can measure this in feet, meters, miles, light-years, whatever. And the time coordinate t, is measured from some arbitrarily chosen event, and you can choose that scale arbitrarily, as well, whether it be seconds, hours, months, or years, whatever.
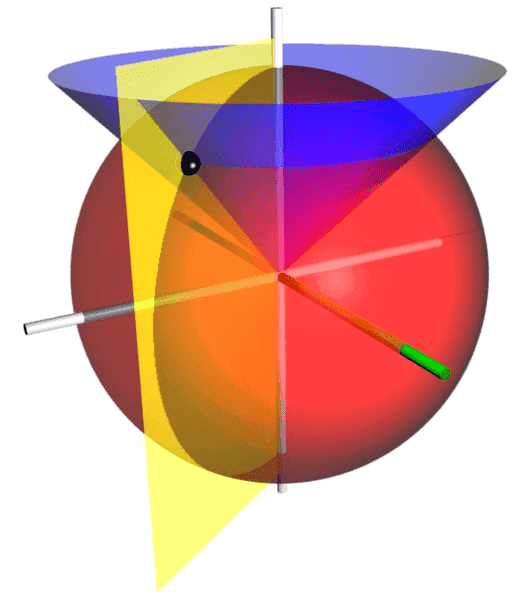
Illustration of spherical coordinates. The red sphere shows the points with r = 2, the blue cone shows the points with inclination (or elevation) θ = 45°, and the yellow half-plane shows the points with azimuth φ = −60°. The zenith direction is vertical, and the zero-azimuth axis is highlighted in green. The spherical coordinates (2,45°,−60°) determine the point of space where those three surfaces intersect, shown as a black sphere.
Second, you can't split up the line element into a "positive" and "negative" part, as though one part calculates dτ and the other part calculates ds. The line element is a single expression for calculating a single interval. Putting dτ vs. ds on the left-hand side is just a naming convention, corresponding to a sign convention for the metric coefficients; typically, if the LHS is written as dτ it means you are using a timelike sign convention, where timelike squared intervals are positive, so the "time" metric coefficient will be positive and the "space" ones will be negative, whereas if the LHS is written as ds it means you are using a spacelike sign convention, where spacelike squared intervals are positive, so the "space" metric coefficients are positive and the "time" one is negative. But "time" and "space" here are in quotes because not all metrics are diagonal and not all metrics have one timelike and three spacelike coordinates. Anyway, the sign convention is just that, a convention; it doesn't affect the physics. Same for the convention of writing the LHS as dτ or ds.
Let ds^2 = -\left ( 1 - \frac{2 G M}{c^2 r} \right )c^2 dt^2 + \left ( 1-\frac{2 G M}{c^2 r} \right )^{-1} dr^2 + r^2 (d\theta^2 + sin^2(\theta)d\varphi^2). If the right-hand-side comes out to be a positive number, then the space-time interval is space-like; meaning there is no way for a clock to move between the two events (t,r,θ,φ) and (t+dt, r+dr, θ+dθ, φ+dφ). But it is possible to stretch a physical object such as a ruler between those two events. On the other hand, if the RHS is negative, then the space-time-interval is time-like, meaning it would be impossible to stretch a ruler between those two events, but it is possible for a clock to be at both of those events at different times. I don't understand what you mean "the sign convention...doesn't affect the physics" If you aren't distinguishing between time-like intervals, and space-like intervals, I can't imagine how you can get any of the other physics right.
You can try to treat them this way, but it won't work. Minkowski coordinates, interpreted in the usual way, require a flat spacetime; they simply won't work the way you want them to work if spacetime is curved. Same for Lorentz transformations.
The t, r, θ, and φ coordinates are a flat spacetime; (well, to be more clear, θ, and φ are obviously curved, but there is no difficulty converting t, r, θ, and φ. of any given event, and converting it to (t,x,y,z) using \begin{align*} x &= r cos(\phi) sin(\theta) \\ y &= r sin(\phi) sin(\theta) \\ z &= r cos(\theta) \end{align*} From there, there is no difficulty performing a lorentz transformation on the flat coordinates,
Yes, exactly. Gravity is everywhere, therefore curvature is everywhere.
It is not difficult to establish where gravity is present, and where gravity is less present. If you take any given gravitating body, and move further and further away from it, the geodesics become straighter and straighter. Also, as you increase the velocity of a body the trajectory becomes straighter and straighter. There is, of course a limiting factor that even light is affected by gravity, However, from far away, it is clear that objects deep in a gravitational well do not move in straight lines. Objects that are further from a gravitational well move in much straighter lines. It may be appropriate to say that no body will ever follow a perfect straight line in the universe, because of gravity. It is not appropriate or correct to say straight lines do not exist. What you have is curvature of a SUBgeometry which is present everywhere, but it can easily be mapped one-to-one; event by event onto a flat geometry.
And the answer is, in a universe with gravity, no, they don't.
No, this is wrong; in fact, again, there are at least two conceptual errors here. First, you are misusing the term "geodesic". In a curved manifold, a "geodesic" is the closest thing you can get to a straight line. There aren't any curves that are straighter. And all geodesics are equally straight, so it makes no sense to say one is straighter than another. I realize that lots of people don't like calling these curves "straight lines", because they aren't Euclidean straight lines; but that's why the term "geodesic" was invented, so we could have a name for curves in curved manifolds that are the closest analogues to Euclidean straight lines; since in a curved manifold there are *no* Euclidean straight lines at all, geodesics are the best we can do.
Try to understand that I am not drawing a line ON the curved manifold. Think of it more like drawing a line on the plane in a flat surface "above" the curved manifold. Unless you can find a situation where the curved manifold curves down under itself, there is a one-to-one mapping from the curved coordinate system to an overlying global flat coordinate system.
https://www.physicsforums.com/attachment.php?attachmentid=40656&d=1320321617
It doesn't matter if the underlying surfaces are curved, so long as none of the particles in the underlying surface go faster than the speed of light in the overlying geometry, in which case there would be causality problems.
But if I am 4 light years from Alpha Centauri, and say some black hole passed between Alpha Centauri and here. What would happen? The light from Alpha Centauri would probably be bent in every which direction, and I would know there were a problem. Let's say also, that somehow the black hole warps the space-time so that an extra light-year of rulers (physical observables) could fit between Alpha Centauri and me.
Here is where I think we differ. I would say what you have is a bunch of really short rulers, but the distance is still only four light years. You say you have to follow all of the curves, and so the distance is five light years. I'm saying there is a global flat coordinate system overlying all of your curved space; you do NOT have to follow all of the curves. You're saying there is no global coordinate system, and the only way to measure distance is to place rulers end to end, and look at clocks you are physically carrying, ignoring the presence of distant bodies.
Second, you are misunderstanding the physics. A geodesic is the worldline of an object on which *no* forces are acting, when the term "force" is defined correctly, as something that is actually *felt* by an object (and which can be measured by an accelerometer). You define gravity as a force, but an object moving solely under the influence of gravity is weightless; it feels no force, and an accelerometer attached to it would read zero. You can call the path of this object "curved" if you like, but it's the straightest path there is in a spacetime with gravity present. If you disagree, then please explain, in detail, how we are to *physically* pick out the "real straight lines", the ones compared to which we are supposed to view the path of a freely falling object as curved. Oh, and by the way, saying that "straight lines" are defined by the paths of light rays will *not* work; light is bent by gravity as well. It isn't bent as much because it moves faster than ordinary falling objects, but its path is still bent. (If you ask why light and a falling rock travel on such different paths if they're both geodesics, that's because there are many geodesics through any given event, corresponding to all the possible velocities a freely falling object can have at that event, up to and including the speed of light.)
For the purposes of a Lorentz Transformation, It doesn't matter whether a body "feels" a force. What matters is whether it undergoes a change in velocity. I fully agree that when an object's path curves under a gravitational field, there is little or nothing it experiences internally. But I don't think we should limit our description of physics to beings so obsessed with themselves that they never look anywhere except at the clock on their navel. The fact is, I do not "feel" the motion of my body around the Earth as it revolves. I do not "feel" the motion of the Earth around the sun. I do not "feel" the motion of the sun around the center of the Milky Way. Yet I am aware of all of these motions . I am aware that these motions are not straight lines. The accelerometer reads zero, but it is still obvious that I am changing velocity, and changing my reference frame.
To explain, in detail, how we are to *physically* pick out the "real straight lines", it's not a question of picking out THE real straight line, it is in distinguishing between lines which are obviously not straight and those which are straighter.
For each of these motions, I can draw a picture of the orbital path, and then I can at draw a tangent line that is MUCH straighter than the geodesic. How will I pick out the real straight lines? For one, by using those variables t, r, θ, and φ, converting them to cartesian coordinates by \begin{align*} x &= r cos(\phi) sin(\theta) \\ y &= r sin(\phi) sin(\theta) \\ z &= r cos(\theta) \end{align*} and then using the usual method for describing straight lines in Cartesian Coordinates.
Well, of course. Are you trying to say an object is moving with respect to itself?
No. What I'm saying is that putting a falling rock in a box that is also falling does not make it move in a straight line. You think that the closest you can get to a straight line is by throwing a rock. That rock is not going in a straight line. It goes up and falls. Ahh, but now you say
"Put the rock in a box. See now, in the box the rock is going in a straight line, relative to the box. Ergo, Hence, Therefore, straight line. QED" or
From inside the box, the rock appears stationary. Therefore, the rock is only traveling through time. Hence a geodesic arc is a straight line. So by putting the rock in a box, now you think the rock is going in a straight line? The rock is NOT going in a straight line. It is just now that you have both rock and box moving in an arc, and because it is (roughly) the same geodesic, it looks like a straight line.
All I'm saying is, don't put the rock in the stupid box. Don't ignore the presence of gravity. Don't put me in a box and throw the box, because regardless of how it "feels" like I must be floating in free space, that doesn't change the fact that I'm going to hit the ground hard, and frankly hitting the ground IS a physical observable.
The reason we pick out τ is that it's a physical observable; it's the proper time experienced by an observer traveling on that worldline. You can't observe t, r, θ, and φ directly. Sometimes you can observe things that are very *close* to those coordinates, but that only works in regions where gravity is very weak. You can't generalize to everywhere in a curved spacetime.
This tyranny of "observables" is overrated. You limit your notion of distance and time to the actual readings of clocks, and the lengths of rulers that you can physically touch. I watch someone throw a rock and it follows a geodesic. To me that path looks curved. You claim that it is not curved, because if we put the rock in a box that were traveling along with it, also following a geodesic, and rulers in the box, then it would appear from inside the box that the rock was not moving; or might be following a straight line.
The point is that it does not matter whether t, r, θ, and φ can be measured directly. We don't actually need to put clocks and rulers out there to get a pretty good idea where the sun is, where the moon is, where Jupiter is, where the center of the galaxy is. (or was when the light left it). The point is, any nonlocal measurement of distance (i.e. the estimation of distance by sight or parallax, or luminosity.)
My point is, it does not make sense to constrain your physics to only things you can touch. You need to think about far-away objects as well. When discussing far-away objects, the distances are not determined by following every curve of the gravitational manifold, but are instead determined by an overlying global flat coordinate system.
