gneill said:
No, that is not the goal of the book. The book presents concepts in sequence as required. It's not likely that you'll be needing to apply the concept of instantaneous radius of curvature until much later. I mentioned it because it was applicable to your query on types of acceleration where a particle is following some general trajectory. In your present studies the radius of curvature that you'll run into will almost invariably be associated with circular motion wherein the curvature remains constant and the concepts of that form of motion are presented fairly early on.
So, I suppose you're also saying that, in this case, it may not be absolutely essential or necessary to have to read the 1000 pages of physics text in order to understand instantenous radius of curvature as it relates to the types of acceleration components that I'm asking about. Its just, as you say, a sequence of concepts the book requires. If understanding instantaneous radius of curvature can bring more clarity to acceleration vectors along a curve, then i'd gladly take the extra time to examine those concepts if they are within my ability to understand it.
I'm going to begin searching for info on instantaneous radius of curvature. In the meantime, I do have a few more questions about acceleration along curves.
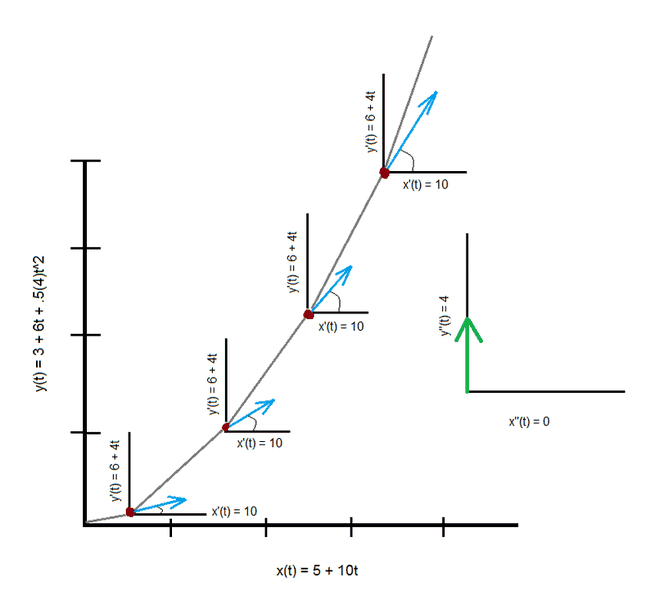
Okay, so, we have established that the x and y-axis position equations as a function of time are the equations that describe motion along a trajectory. And if one or both of those position equations are to the power of 2, then there will be some constant acceleration in some direction. So, in regard to:
gneill said:
That is true, yes. Note that there may be other acceleration, too. In keeping with the notion of perpendicular coordinate systems and therefore perpendicular vector components, there could also be a "linear" acceleration tangent to the curve at that that same instant. If centripetal acceleration is constant and non-zero for all time, and linear acceleration is constant and zero for all time, then you have true circular motion.
Then it should be able to be said that since the motion of an object follows the position equations, if the position equations represented the path of a circle, then an object would have a circular motion.
However, coming up with an equation that describes the path of a circle as a function of time is proving difficult. I know the equation of a circle is r = \sqrt{(x-h)^2 + (y-k)^2}. But that is not a function. It can be made into a piecewise function where f(x) = ±√(1-x^2), but I don't think that describes position in terms of x and y components on a graph, nor does it seem to describe position as a function of time.
If I could find an equation for both x and y axes that describes motion of a circle, it would seem I could then take the second derivative of those functions and calculate circular acceleration as a function of time.
So the problem here is: how could I find an x and y components of a position equation as a function of time that describes a circlular motion?