peripatein
- 868
- 0
Hello,
I'd like to please verify whether my solution to the problem as described below is indeed correct.
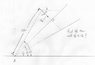
Ship A is traveling east at a constant velocity of 30km/h. It notices ship B 15 km away and 30° from the north. Ship B is traveling at a constant velocity. 20 minutes later ship A notices ship B 45° from the north, and 20 more minutes after that ship B is observed 60° from the north. The distance between ship A and B at that point in time ought to be calculated, including the velocity (magnitude and direction) of ship B.
Proposed solution:
Supposing ship A first spots ship B from O, (0,0):
1) (1/3Va)(OB + 1/3Vb) / |(1/3Va)||(OB + 1/3Vb)| = 1/SQRT(2)
2) (2/3Va)(OB + 2/3Vb) / |(2/3Va)||(OB + 2/3Vb)| = SQRT(3)/2
[Va, Vb, OB are vectors; 1/SQRT(2) = cos 45°; SQRT(3)/2 = cos 30°]
I got Vb = (27.56,15.91), |Vb| = 31.82 km/h, distance between ship A and B 40 minutes later = 12.14 km
Are these equations correct? Is their solution?
I'd like to please verify whether my solution to the problem as described below is indeed correct.
Ship A is traveling east at a constant velocity of 30km/h. It notices ship B 15 km away and 30° from the north. Ship B is traveling at a constant velocity. 20 minutes later ship A notices ship B 45° from the north, and 20 more minutes after that ship B is observed 60° from the north. The distance between ship A and B at that point in time ought to be calculated, including the velocity (magnitude and direction) of ship B.
Proposed solution:
Supposing ship A first spots ship B from O, (0,0):
1) (1/3Va)(OB + 1/3Vb) / |(1/3Va)||(OB + 1/3Vb)| = 1/SQRT(2)
2) (2/3Va)(OB + 2/3Vb) / |(2/3Va)||(OB + 2/3Vb)| = SQRT(3)/2
[Va, Vb, OB are vectors; 1/SQRT(2) = cos 45°; SQRT(3)/2 = cos 30°]
I got Vb = (27.56,15.91), |Vb| = 31.82 km/h, distance between ship A and B 40 minutes later = 12.14 km
Are these equations correct? Is their solution?