Q: "Time Dilation: Faster = Longer Wait?

[Semifaded]

Time Dilation problem

I understand Time Dilation and most of the principals involved. However I am still stuck on this one lingering question that I can’t make sense out of. If anyone could answer this I would really appreciate it.

Given:
1. Person A is the traveler

2. Person B is stationary

The next two are calculated via the Lorentz Transformation

3. If Person A travels at 50% the speed of light then one year for Person A is equivalent to 1.15 years for Person B

4. If Person A travels at 99.99% the speed of light then one year for Person A is equivalent to 70.71 years for Person B

Here’s the lead up to my question:

Person A is going to the best burrito shop in the galaxy located on Planet X. This planet is exactly one light year away. He will bring back two burritos for himself and Person B to eat. Let’s calculate how long Person B will be waiting.

If Person A travels at 50% the speed of light it will take 4 years to return (two years over and two years back). By this time 4.60 years would have passed for Person B (4x1.15)

If Person A travels at 99.99% the speed of light it will take 2 years to return (It will take a tiny bit longer than two years but this discrepancy is negligible for this problem). In this scenario 141.42 years would have passed for Person B (2x70.71).

Which brings me to the question:
If I send someone to get me lunch on another planet, the faster they travel the longer I have to wait?

 

[Ibix]

When you say "it takes x amount of time for something to happen" you must always ask "x amount of time for who?". That's what has tripped you up here.

If Person A travels at 50% the speed of light it will take 4 years to return (two years over and two years back). By this time 4.60 years would have passed for Person B (4x1.15)

It would take four years by whose watch?

If Person A travels at 99.99% the speed of light it will take 2 years to return (It will take a tiny bit longer than two years but this discrepancy is negligible for this problem). In this scenario 141.42 years would have passed for Person B (2x70.71).

It would take two years by whose watch?

What you appear to have done is calculated the travel time as seen by the stay-at-home person B, assumed that that travel time will show on person A's watch when he returns, and then calculated the time that would show on person B's watch if that assumption were correct. It's not correct - you know the time on person B's watch (4 years or 2 years) and you need to calculate the time on person A's watch.

Both the distance traveled and the time taken are different for person A and person B. According to B, who stays at home, Person A goes out at 0.5c and returns in four years (he had two light years to cross and t=d/v) but Person A's watch will read γt=0.866×4=3.46 years. According to person A, the burrito shop traveled to him at 0.5c, but it only traveled γd=0.866×2=1.73 light years, so he has no problem with his watch coming up at less than 4 years.

You can do the calculations for 0.9999c. There will be a bigger discrepancy between the watches, but the same thing will happen as above.

 

[Semifaded]

Thanks for the response IBIX. Sorry, but perhaps I didn't make this one point clear enough. Planet X is Exactly one light year away.So if Person A travels 50% the speed of light to a planet that is one light year away it will take him two years to reach the planet and two years to return.

1. If Person A travels the speed of light then it will take that person one year to reach the planet and one year to return. Same as if Person A was traveling 99.99% the speed of light minus the negligible difference.

2. Now that I know the exact amount of time that has passed for Person A, I can calculate the amount of time that has passed for stationary Person B

3. If Person A travels at 50% the speed of light then one year for Person A is equivalent to 1.15 years for Person B

4. If Person A travels at 99.99% the speed of light then one year for Person A is equivalent to 70.71 years for Person B

Are any of these four "givens" incorrect?

 

[Doc Al]

So if Person A travels 50% the speed of light to a planet that is one light year away it will take him two years to reach the planet and two years to return.

Careful. It is person B who sees person A as traveling at 50% the speed of light. So, according to person B's clocks the trip takes 4 years. According to person A the trip is shorter.

 

[Nugatory]

Planet X is Exactly one light year away.
So if Person A travels 50% the speed of light relative to person b to a planet that is one light year away as measured by person B it will take him two years as measured by person B's clock to reach the planet and two years as measured by person B's clock to return.

1. If Person A travels nearly the speed of light relative to person b then it will take that person one year to reach the planet as measured by person B's clock and one year as measured by person B's clock to return. Same as if Person A was traveling 99.99% the speed of light minus the negligible difference.

I've made the necessary additions in boldface.

2. Now that I know the exact amount of time that has passed for Person A, I can calculate the amount of time that has passed for stationary Person B.

You have it backwards. You know the time that passed as measured by person B, and you can calculate what person A, the traveller, experiences.

 

[Ibix]

Number 1 is wrong. If planet X is exactly 1ly away according to the stay-at-home person, it is 0.866ly away according to the traveller - length contraction at work. It is the stay-at-home whose watch shows 4 years when the traveller returns - the traveller's watch shows less time. You have the time dilation factor correct, but are applying it backwards here.

If I may, I think that you haven't quite grasped special relativity quite as well as you think. You keep saying things like "the distance is x" and "the time is t" without specifying whose distance or whose time. The key point about SR is that two people who are not at rest with respect to each other do not, in general, agree on positions, lengths, times, and a host of other quantities. Saying "planet X"is 1ly away is not enough - you must say 1ly away according to person B (or whoever).

I have been assuming that you mean planet X is 1ly away according to the stay-at-home person B, because he is the only constant in your problem. But you didn't specify, and it is that lack of clear thinking about who exactly is measuring what that is leading to your confusion.

Edit: I obviously type too slow. Nugatory and Doc Al have rendered my response... er... nugatory.

 

[Semifaded]

OK Thanks Doc, Ibix and Nugatory. You guys helped clear up my confusion. I understand where I was making the mistake now.

 

[Warp]

Btw, the key point why A and B measure different traveling times is not really the speed at which one of them travels (because from A's perspective it's B who is moving and from B's perspective it's A who is moving, so the situation is symmetrical). The crucial difference is the acceleration from one speed (B's) to another (A's first acceleration away from B, then after a time a new acceleration back towards B). The acceleration causes a change in frames of reference.

(This is the answer to the so-called twin paradox.)

 

[ghwellsjr]

Btw, the key point why A and B measure different traveling times is not really the speed at which one of them travels (because from A's perspective it's B who is moving and from B's perspective it's A who is moving, so the situation is symmetrical). The crucial difference is the acceleration from one speed (B's) to another (A's first acceleration away from B, then after a time a new acceleration back towards B). The acceleration causes a change in frames of reference.

(This is the answer to the so-called twin paradox.)

It's true that B accelerates but that doesn't mean there must be a change in frames of reference in order to answer the so-called twin paradox. You can use any Inertial Reference Frame (IRF) and get the correct answer. Here are three IRF's based on the OP's first scenario at 50% of light speed to show you what I mean.

First, in the IRF in which both A and B start out at rest. B (black) travels at 50%c for 1 light-year and then returns. Note that it takes him 21 months according to his clock to get to Planet X and another 21 months to return. Since his speed in this IRF is 0.5c, his time dilation 1.1547 which means that the dots marking off each month are spaced slightly farther apart than the coordinate months. Meanwhile, A (blue) has aged by 48 months. (I have made B travel exactly 21 months to get to Planet X which is a little long and so A has aged a little long also.) B's total aging is 42 months while A's is a little over 48 months.

That is all that is necessary to explain the scenario. However, we can transform the entire scenario into another IRF and show it all over again. Here is the IRF in which B is stationary during his trip to Planet X. During this time, he is experiencing no time dilation and his months proceed in step with the coordinate time. However, A is traveling away from him at 0.5c according to the IRF so his time is dilated by the factor 1.1547. After 21 months, B turns around and heads for home. However, he now has to travel at 0.8c according to the IRF so his time is now dilated by 1.6667. When he arrives back home, A has aged slightly more than 48 months and B has aged 42 months, exactly like in the first IRF.

Now we can do another transformation and see what the scenario looks like in the IRF in which B is stationary for his return trip:

This looks very much like the previous IRF and the numbers apply in a similar manner so I won't go into the details.

Please note that each IRF is self-contained and explains everything about the scenario. Each IRF can easily handle the three accelerations that B experiences without the need to jump between frames or use a non inertial reference frame. If you want to claim that these IRF's do not explain the OP's scenario (or the so-called twin paradox) then I invite you to describe what you think is wrong with them and then produce your own detailed explanation and hopefully a plot to illustrate your explanation.

 

[K^2]

The point on acceleration is to answer the question, "Why can't we use the frame in which B is stationary all the time?" Answer being that you can, but it's not an inertial frame, so SR is insufficient to describe it. But any inertial frame should certainly give you consistent answers with SR alone.

 

[Darwin123]

Time Dilation problem

I understand Time Dilation and most of the principals involved. However I am still stuck on this one lingering question that I can’t make sense out of. If anyone could answer this I would really appreciate it.

Given:
1. Person A is the traveler

2. Person B is stationary

The next two are calculated via the Lorentz Transformation

3. If Person A travels at 50% the speed of light then one year for Person A is equivalent to 1.15 years for Person B

4. If Person A travels at 99.99% the speed of light then one year for Person A is equivalent to 70.71 years for Person B

Here’s the lead up to my question:

Person A is going to the best burrito shop in the galaxy located on Planet X. This planet is exactly one light year away. He will bring back two burritos for himself and Person B to eat. Let’s calculate how long Person B will be waiting.

If Person A travels at 50% the speed of light it will take 4 years to return (two years over and two years back). By this time 4.60 years would have passed for Person B (4x1.15)

If Person A travels at 99.99% the speed of light it will take 2 years to return (It will take a tiny bit longer than two years but this discrepancy is negligible for this problem). In this scenario 141.42 years would have passed for Person B (2x70.71).

Which brings me to the question:
If I send someone to get me lunch on another planet, the faster they travel the longer I have to wait?

It depends on what you call "faster". "Faster" can mean "great speed" or "greater acceleration." So there is a clearer way to present the same idea.

The more they accelerate, the longer I have to wait.

Here, acceleration refers to the dynamic acceleration which is force on the traveler divided by mass of the traveler. Also, deceleration is equivalent to acceleration. The issue comes down to the force on the traveler.

In the case of the twin scenario, it turns out to be the same thing. If the rocket travels with great velocity, then it has have a very large acceleration toward Earth in order to turn around.

For me, the weird thing was this is a nonlocal effect. Weird= antiintuitive. Basically, the person in the rocket ages the one on Earth merely by using his rockets to turn around. Although this is weird, it logically works out. It seems a little strange that the twin by running his rockets a large distance away makes the twin on Earth instantly age faster. However, this is an illusion in the following sense. The speed of light is the fastest possible speed in the universe. Therefore, the twin in the rocket can't immediately know that the twin aged faster while the rockets were running.

Basically, the traveler which has the biggest impulse ages the slowest. Impulse equals integral of force with time = change in linear momentum due to force. The Earth twin never has a force applied to him, so he ages fastest.

The Lorentz time dilation formula is expressed in terms of the speed of the traveler. However, hidden in the derivation of this formula is the dynamic acceleration. The "logical adjustments" in the physics occur while the twin in the rocket is turning around.

Another problem is with the twin scenario itself. To simplify the concepts, the twin conundrum is expressed in the extreme limit of an instantaneous turn around. This makes the math a lot easier, compared to if it was a slow turn around. However, an instantaneous turn around is impossible. An instantaneous turn around would squash the traveling twin into a quark plasma! The acceleration is important but hidden in the set up of the problem.

The problem with a slow turn around is it takes more time. The traveler feels less force, but he feels it over a much longer time. The two effects cancel out so that the Lorentz contraction still works, even with the slow turn around.

The physical symmetry is broken by the impulse on the traveler. The observer experiencing the greatest impulse ages slowest.

There are some physicists who state that there is no acceleration in relativity. However, they mean it in a very technical sense. The Lorentz time dilation formula doesn't explicitly contain acceleration. It contains only speed. However, the dynamic acceleration is subtly implied.

 

[Ibix]

I'm almost afraid to start this.

The more they accelerate, the longer I have to wait.

I'd love to see the maths supporting that statement, because it seems to me to be incorrect. If I send out two people to get burritos, and one accelerates harder than the second then he will always be ahead of the second guy, and will return sooner.

For me, the weird thing was this is a nonlocal effect. Weird= antiintuitive. Basically, the person in the rocket ages the one on Earth merely by using his rockets to turn around. Although this is weird, it logically works out. It seems a little strange that the twin by running his rockets a large distance away makes the twin on Earth instantly age faster.

I'm fairly certain this isn't true, either. Consider the cash going out to the burrito shop floating free, and the burrito coming back the same way. According to me, the cash takes t₁=d/v to get to the shop and the burrito takes t₂=d/v to get back. According to a clock traveling with the cash, it takes t₁'=d/(γv) to get to the shop; according to a clock traveling with the burrito it takes t₂''=d/(γv) to get back to me. My total wait is 2d/v; the total travel time of the cash and burrito is 2d/(γv).

The key point here is that the acceleration phase of the cash and the burrito is completely irrelevant - it happens outside the scope of the experiment and can be as hard or as gently as you like. You can even imagine a universe empty except for me, the burrito shop and some cash and a burrito created (fiat burrito) at the correct velocities. You still find that the total elapsed time for the travellers is less than that for the stay-at-home.

It isn't the acceleration that "causes" the difference. For a single observer to follow the path of the cash-and-burrito, they do need to accelerate, but the difference in elapsed time is due to the two observers following unequal length paths through spacetime. A good analogy is me driving from A to B in a straight line, while you drive from A to C to B. Certainly you can't get to B without making a turn at C, but that turn doesn't "cause your path to be longer"; it just is longer because it's not the direct route.

 

[K^2]

I'd love to see the maths supporting that statement, because it seems to me to be incorrect. If I send out two people to get burritos, and one accelerates harder than the second then he will always be ahead of the second guy, and will return sooner.

It happens to be wrong in OP's example, but don't just assume things are always going to be so clear cut.

Imagine that two people on a space station orbiting a planet want to go get burritos that are sitting on a station half a revolution ahead. They both get into their shuttles. One gives a short burn forward to accelerate, the other gives a short burn in reverse to slow down. About half way, they adjust their orbits again to intercept the station with burritos. Which one gets to burritos first? One that initially slowed down. Why? Because he took a shorter, faster path.

 

[Ibix]

It happens to be wrong in OP's example, but don't just assume things are always going to be so clear cut.

I wasn't assuming, although I should have explained my reasoning, which is as follows. In a flat space in the low-velocity limit, Darwin123's contention is obviously wrong. As far as I am aware, the acceleration observed in an inertial frame when a body undergoes proper acceleration of a' is a=a'/γ³ - and that doesn't let a slower-accelerating body overtake a faster accelerating one either.

Imagine that two people on a space station orbiting a planet want to go get burritos that are sitting on a station half a revolution ahead. [snip] Which one gets to burritos first? One that initially slowed down. Why? Because he took a shorter, faster path.

I know enough orbital mechanics (including that result, as it happens) to know that intuition is risky (at best) there. I dread to think what general relativistic orbital mechanics looks like.

 

[Darwin123]

I'm almost afraid to start this.

I'd love to see the maths supporting that statement, because it seems to me to be incorrect. If I send out two people to get burritos, and one accelerates harder than the second then he will always be ahead of the second guy, and will return sooner.


I'm fairly certain this isn't true, either. Consider the cash going out to the burrito shop floating free, and the burrito coming back the same way. According to me, the cash takes t₁=d/v to get to the shop and the burrito takes t₂=d/v to get back. According to a clock traveling with the cash, it takes t₁'=d/(γv) to get to the shop; according to a clock traveling with the burrito it takes t₂''=d/(γv) to get back to me. My total wait is 2d/v; the total travel time of the cash and burrito is 2d/(γv).

The key point here is that the acceleration phase of the cash and the burrito is completely irrelevant - it happens outside the scope of the experiment and can be as hard or as gently as you like. You can even imagine a universe empty except for me, the burrito shop and some cash and a burrito created (fiat burrito) at the correct velocities. You still find that the total elapsed time for the travellers is less than that for the stay-at-home.

It isn't the acceleration that "causes" the difference. For a single observer to follow the path of the cash-and-burrito, they do need to accelerate, but the difference in elapsed time is due to the two observers following unequal length paths through spacetime. A good analogy is me driving from A to B in a straight line, while you drive from A to C to B. Certainly you can't get to B without making a turn at C, but that turn doesn't "cause your path to be longer"; it just is longer because it's not the direct route.

Round trip time and turn around time are different. Round trip time is the total time the round trip takes. The turn around time is the time the external force is working on the observer. In the twin conundrum, the external force on the traveling twin is the thrust of the rockets.

The so called paradox is in round trip time. Newtonian physics says that the round trip time is the same for both twins. Relativity says that if the relative speed of the two is ever close to the speed of light, then the round trip time is longer for the twin on earth. This is what we call an asymmetry.

There is no asymmetry in your burrito example. In your burrito example, at low speed, both observers have to wait the same amount of time during the round trip. The one who went out to get the burrito is just as old as the one who waited for the burrito. Acceleration shortens the round trip time the same way for both observers.

A higher nonrelativistic velocity may shorten the turn around time for both. However, the time it takes to turn around, which was defined in terms of force, will be longer if the one who goes out is running. Newton's first law says that a body in motion tends to stay in motion unless acted on by an outside force. In order to turn around, he has to accelerate in the opposite direction. He can either turn around suddenly with great force or turn around slowly with less force. The time is the same for both.

At high speeds close to the speed of light, the round trip time is different for both observers. The time that the rocket engines are on gets longer for both observers if the twin in the rocket starts moving at high speed. However, the asymmetry between observers is made while the rocket engines are on.

The rocket engine does something in relativity to the clocks and rulers of the accelerating twin that isn't done to the clocks and rulers in Newtonian physics. The rockets make an asymmetry that can only be seen after the round trip.

 

[K^2]

I dread to think what general relativistic orbital mechanics looks like.

Surprisingly benign, so long as you stay above 3r_s.

 

[Ibix]

However, the asymmetry between observers is made while the rocket engines are on.

Ghwellsjr's spacetime diagrams already demonstrate that this isn't true. Let his blue line be the worldline of the stay-at-home, one of the black legs be the worldline of the outbound cash, and the other black leg be the worldline of the inbound burrito. His diagrams accurately describe my scenario, and the proper time experienced by the cash on its trip plus the proper time experienced by the burrito on its trip total less than the proper time of the stay at home person, with no acceleration involved.

I note that you haven't posted maths or references to back up your claim that greater acceleration leads to a longer wait time for the stay at home twin. It seems wrong to me for reasons I articulated in my response to K^2. Could you let me know (with maths) what it is that you think happens? What is the parameter that determines when the Newtonian result (higher acceleration gets there in less time) gives way to your regime?

 

[Mentz114]

... I dread to think what general relativistic orbital mechanics looks like.

It looks very good. This paper has the maths and some good orbital plots.

:http://arxiv.org/pdf/1201.5611v1.pdf

 

[Darwin123]

Ghwellsjr's spacetime diagrams already demonstrate that this isn't true. Let his blue line be the worldline of the stay-at-home, one of the black legs be the worldline of the outbound cash, and the other black leg be the worldline of the inbound burrito. His diagrams accurately describe my scenario, and the proper time experienced by the cash on its trip plus the proper time experienced by the burrito on its trip total less than the proper time of the stay at home person, with no acceleration involved.

I note that you haven't posted maths or references to back up your claim that greater acceleration leads to a longer wait time for the stay at home twin. It seems wrong to me for reasons I articulated in my response to K^2. Could you let me know (with maths) what it is that you think happens? What is the parameter that determines when the Newtonian result (higher acceleration gets there in less time) gives way to your regime?

Most of these mathematical proofs using GR rely on one path being a geodesic and the other not a geodesic. The twin on Earth is traveling a geodesic, which is the shortest path in space time between two point. The traveling twin is not on a geodesic. His path is not on the shortest path through space time.

Ghwellsjr's spacetime diagrams would not be satisfying because the diagram couldn't show the symmetry breaking mechanism. This is a case where a word could be worth a thousand pictures. Even if the analysis was mathematical, what would be useful is if the equation with the symmetry breaking mechanism was presented. At least one would get an idea of how the symmetry breaking occurred.

The problem is that there is no physical hypothesis that distinguishes between trajectories that are geodesics and trajectories that are not geodesics. One can always find a set of variables in which an observer is traveling a geodesic. After all, the physical laws are independent of the path of the observer. "Everything" is relative, or so people have been told.

What many people are asking is not whether there is mathematics that distinguish one twin from the other. They are asking for a physical hypothesis that distinguishes between the two observers. They want to know the "symmetry breaking" feature in the calculation. "Physical intuition" is not sufficient for distinguishing between a geodesic and a nongeodesic.

Many books on science for laymen say straight out that it is the rockets that break the symmetry. I am just generalizing what these books in "mainstream science" say. Instead of "rockets", I say "external force". What you seem to be saying is that the rockets have nothing to do with the twin on Earth aging faster than the traveling twin. What is asked for is a physical hypothesis, not a mathematical proof. The mathematical proof is certainly worth a discussion on its own, but it is irrelevant here.

There are many problems in physics where a symmetry is broken. The question of what interaction physically breaks a symmetry is often a valid scientific question, regardless of scientific field.

 

[K^2]

Most of these mathematical proofs using GR rely on one path being a geodesic and the other not a geodesic. The twin on Earth is traveling a geodesic, which is the shortest path in space time between two point. The traveling twin is not on a geodesic. His path is not on the shortest path through space time.

Longer path would mean longer proper-time, which would mean that twin that traveled aged more than the twin that remained in one place.

The fact is, twin that traveled has actually taken a shorter path. How? Geodesics are local minima. In fact, they don't even have to be minima, merely extrema, but I don't know if that's ever relevant in GR. At any rate, there can exist paths that are shorter.

For a simple analogy, think of an object in a glass of water placed in such a way that you can see the object both through the wall of the glass and through the surface. It looks like there are two copies of the object, one distorted more than the other. I'm sure you've seen this. In optics, light takes the "shortest" path as well. Fact that you can see two images of the same object tells you that there are two "shortest" paths between the object and your eye. Again, the path only needs to be locally shortest. Meaning that any small perturbation of the path has to increase the length.



Anyways, back to the twins. I'm not entirely sure whether it's fully equivalent to engine thrust, but imagine that the twin that traveled used gravity of a massive object, like a black hole, to turn around. That way, his trajectory is also a geodesic. It is also locally shortest. However, the question of which path is shorter remains.

We know the answer, of course. Special Relativity tells us that the twin that stayed put aged more. That means, his path was longer.

 

[PeterDonis]

The fact is, twin that traveled has actually taken a shorter path. How? Geodesics are local minima.

No, they are local *maxima*. But in flat spacetime, which is what seems to be the assumption in this thread, a local maximum is also necessarily a global maximum. The possibility of multiple extremal paths, which you refer to later on in your post, only exists in curved spacetime.

The reason the traveling twin's path is shorter is the Lorentzian analog of the triangle inequality: two sides of a triangle are *shorter* than the third, if all three sides are geodesic segments. Physically, this corresponds to the fact that the motion of the traveling twin, who travels along two sides of the triangle, can't be geodesic everywhere; there must be at least one event where he undergoes non-geodesic motion. Only the stay-at-home twin, who moves along only one side of the triangle, can have a path that is geodesic everywhere, so his path is necessarily the longest.

imagine that the twin that traveled used gravity of a massive object, like a black hole, to turn around. That way, his trajectory is also a geodesic. It is also locally shortest. However, the question of which path is shorter remains.

We know the answer, of course. Special Relativity tells us that the twin that stayed put aged more. That means, his path was longer.

Only if you assume that the gravity of the massive object is negligible throughout most of the spacetime; in other words, that the spacetime is flat everywhere except for a very small region around the massive object. Then in that flat spacetime, the path of the traveling twin is *not* a geodesic, which is why SR says the stay at home twin ages more. The massive object in this scenario just takes the place of the rocket or whatever it is that turns the traveling twin around; you're not actually making use of the curvature of spacetime around it except as a "rocket substitute".

If, OTOH, you want to have a scenario where the curvature of spacetime around the massive object is the primary effect, it is easy to construct one where the "stay at home" twin ages less. Just have the stay at home twin be in orbit about the massive object, and have the traveling twin be launched directly upward in such a way that he is pulled back down by the massive object's gravity to meet the stay at home twin after some integral number of orbits. Here both twins are traveling along geodesics, so it is clearer what the difference is between a local maximum and a global one.

 

[PeterDonis]

The problem is that there is no physical hypothesis that distinguishes between trajectories that are geodesics and trajectories that are not geodesics. One can always find a set of variables in which an observer is traveling a geodesic.

No, you can't. The path of the traveling twin cannot be geodesic everywhere. (At least, not in the standard version; as K^2 pointed out, and I amplified in my response to him, in curved spacetimes one can set up scenarios where there are multiple geodesic paths between the same pair of events, with different lengths. But in flat spacetime, meaning wherever gravity is negligible, there is only one geodesic path between any pair of events, and it is the path of maximal proper time.)

Physically, what "the path of the traveling twin cannot be geodesic everywhere" means is that the traveling twin has to turn around somehow. If spacetime is flat (i.e., gravity is negligible), the only way he can do that is by firing rockets, getting pushed by a laser, etc.--i.e., he has to experience a force, even if only for an instant (in the idealized version of the scenario that you've been discussing, where the turnaround is instantaneous). This means that an accelerometer carried with the traveling twin will read nonzero, even if only for an instant. The stay at home twin's accelerometer will read zero the entire time.

"Physical intuition" is not sufficient for distinguishing between a geodesic and a nongeodesic.

No, but a direct physical measurement made with an accelerometer is. See above.

 

[PeterDonis]

with no acceleration involved.

This is not strictly true. Something has to change direction, and that requires acceleration. In your version, the "something" is information; nothing physical actual changes direction in your scenario. But you are describing the traveling worldline (burrito + cash) in two different inertial frames; the inertial frame in which the cash is at rest outbound is different from the inertial frame in which the burrito is at rest inbound. That is equivalent to having an acceleration somewhere; "acceleration" may not be the best word, but we don't really have another term for "switching inertial frames midstream".

 

[Ibix]

Many books on science for laymen say straight out that it is the rockets that break the symmetry.

You are reading too much into this statement, I think. The setup usually assigns specific tasks to each twin (sit on Earth, fly to Alpha C), for easy identification. But if you strip that away by putting both twins in rocket ships, performing symmetric accelerations so that they are separating at speed v, and then leaving them to coast for a while then there is nothing to identify one twin as the stay-at-home and the other as the traveller. You can only tell when one of the twins (chosen by a private agreement between the twins before the experiment begins) fires his engines to turn round and catch up with his sibling.

In that very limited sense, the symmetry is broken by the rockets firing, because that is when everyone can work out who will be the younger twin. But, physically, there is nothing special about the rockets firing. They don't "cause the other twin to age". They just enable the twins to meet up again, which they can't in inertial frames.

The analogy that I made earlier, of driving in a straight line from A-to-B compared to driving A-to-C-to-B is perfectly valid. It isn't the act of turning at C that makes the path lengths different, it is the decision to take a different route through space to the same destination. And if you (a third-party) are ignorant of the destination, you can't tell until one car turns which one is going to, so you cannot predict which will have the higher mileage.

That's exactly what ghwellsjr's spacetime diagrams are showing you. If you hide the top half of them, the first two graphs just look like mirror images of each other. It's only at the point that the rocket fires and one twin turns around that they start to look like different graphs.

 

[Darwin123]

Physically, what "the path of the traveling twin cannot be geodesic everywhere" means is that the traveling twin has to turn around somehow. If spacetime is flat (i.e., gravity is negligible), the only way he can do that is by firing rockets, getting pushed by a laser, etc.--i.e., he has to experience a force, even if only for an instant (in the idealized version of the scenario that you've been discussing, where the turnaround is instantaneous). This means that an accelerometer carried with the traveling twin will read nonzero, even if only for an instant. The stay at home twin's accelerometer will read zero the entire time.



No, but a direct physical measurement made with an accelerometer is. See above.

I agree with the sentences after the word, "Physically". The path of the traveling twin can not be a geodesic everywhere. However, geodesic is a mathematical term which isn't very useful to the experimenter or engineer. In terms of kinematics (i.e., without physical interaction), there is no reason that the twin on Earth has to one a geodesic everywhere. What I meant by "physical" is a local measurement that can determine where the path is not geodesic.

Your comment about the accelerometer is very pertinent. I believe that you have proven my point. What breaks the symmetry is a type of acceleration, just as I said. However, it can't be any type of acceleration. A kinematic acceleration, meaning an acceleration not associated with an interaction, can't break the symmetry.

The physical quantity that determines where the path is not geodesic is whatever the accelerometer is measuring. I submit that the accelerometer is measuring the total force on the accelerometer applied by the surroundings.

The accelerometer is measuring the external force on it by other particles. The observer who is close to the accelerometer and stationary relative to the accelerometer is also under the influence of a force. There may be an accelerometer that is stationary and close to the observer on earth. That accelerometer does not detect an external force.

The quantity that the accelerometer is measuring is what I call the dynamic acceleration. I haven't found a reference that uses that phrase. However, I do see scientists refer to the external force. I think the external force is what breaks the symmetry in the twin paradox. The external force usually stated in the twin paradox is caused by the rockets.

 

[Ibix]

This is not strictly true. Something has to change direction, and that requires acceleration. In your version, the "something" is information; nothing physical actual changes direction in your scenario. But you are describing the traveling worldline (burrito + cash) in two different inertial frames; the inertial frame in which the cash is at rest outbound is different from the inertial frame in which the burrito is at rest inbound. That is equivalent to having an acceleration somewhere; "acceleration" may not be the best word, but we don't really have another term for "switching inertial frames midstream".

Agreed - especially about acceleration not being quite the right word. But if there are no rockets firing, it's not the rockets that are causing the difference, which Darwin123 was claiming and I was refuting. And it's not the transmission of the information that causes the difference either - it's the choosing to follow a different route to get to the same point that results in the journeys having different lengths (or different intervals, in SR language).

 

[Darwin123]

Agreed - especially about acceleration not being quite the right word. But if there are no rockets firing, it's not the rockets that are causing the difference, which Darwin123 was claiming and I was refuting. And it's not the transmission of the information that causes the difference either - it's the choosing to follow a different route to get to the same point that results in the journeys having different lengths (or different intervals, in SR language).

The word "choosing" implies that there is someone doing the choosing. Who is doing the choosing?

Maybe I was saying it wrong. I started out using the word acceleration. Maybe this isn't the right word either.

Whatever physical interaction defines the path of the hypothetical observer is what breaks the symmetry. It doesn't have to be a canonical force. In the case of quantum systems, there may not be a canonical force. Maybe it is a measurement, or a decoherence, or some other type of interaction.

I was not claiming that the rockets cause the aging. I was claiming that the rockets caused the difference in ages. The question was what caused the asymmetry. I claim that the force of the rockets cause the asymmetry.

What physical thing do you think is the cause of the asymmetry? A space time diagram by itself is not enough. If you must present a diagram, circle the part of the diagram which has the physical cause of the asymmetry.

The concrete example in the OP's question involved twins, rockets, and aging. Later it turned in burritos, sidewalks and deliveries. The question was originally about the cause of asymmetry, not about twins or burritos.

 

[ghwellsjr]

...
I was not claiming that the rockets cause the aging. I was claiming that the rockets caused the difference in ages. The question was what caused the asymmetry. I claim that the force of the rockets cause the asymmetry.

The rockets cause a difference in the velocity of a spaceship. Depending on the arbitrarily selected IRF, this velocity change can result in an increase, a decrease, or no change in the speed of the spaceship and therefore a decrease, an increase or no change in the aging rate of the traveler. The aging rate is another word for time dilation and is not observable or measurable by either of the persons or anyone else that might be involved in the scenario.

Your concern over asymmetry or a broken symmetry is a red herring. It only seems relevant in the classic Twin Paradox because one twin remains inertial. But in general, we can have any number of observers starting at one location and traveling at different speeds in different directions and ending up in the same location (but not necessarily where they started) where there is no symmetry in the scenario at all and yet we can still analyze the scenario using any arbitrary IRF and determine how each one ages with respect to each other.

What physical thing do you think is the cause of the asymmetry? A space time diagram by itself is not enough. If you must present a diagram, circle the part of the diagram which has the physical cause of the asymmetry.

I could present an asymmetrical scenario to you in which the twins end up the same age. What question would you ask in this situation?

A spacetime diagram is simply a way to present a whole lot of data in an easily graspable way. It is part of the discipline of the Theory of Special Relativity.

But you don't need to analyze scenarios like this using Special Relativity. You can do it simply with a Relativistic Doppler Analysis which shows physically what each person actually observes and measures. But you have to discipline yourself and not ask about physical causes beyond what can actually be measured and observed so I doubt that that would be satisfying to you either.

The concrete example in the OP's question involved twins, rockets, and aging. Later it turned in burritos, sidewalks and deliveries. The question was originally about the cause of asymmetry, not about twins or burritos.

The OP did not present his question in the context of the Twin Paradox but he did ask about fetching burritos. He did not ask about asymmetry or its cause. He asked an ill formed question which didn't make sense to him (because it didn't make sense to anyone) and was straightened out to his satisfaction by post #7.

Warp was the one that turned this thread into yet another Twin Paradox issue and I corrected him on some false notions and I'm still trying to correct false notions.

 

[bobc2]

...The aging rate is another word for time dilation and is not observable or measurable by either of the persons or anyone else that might be involved in the scenario...

I think this is questionable. One might think that through a little more carefully. You seem to be bringing philosophy into the mix (which I know you typically resent). By your apparent reasoning it would seem that no kind of observation or measurement is possible.

 

[Vandam]

The aging rate is another word for time dilation and is not observable or measurable by either of the persons or anyone else that might be involved in the scenario.

Time dilation not observable? Where do you get this? This is simply wrong.
In another thread I recently tried to explain and show you that time dilation is due to relativity of simultaneity.
https://www.physicsforums.com/showpost.php?p=4189092&postcount=38
The reason you do not understand this is probably because you are too much stuck to your calculator. (And I'm afraid at the end we will have to discuss what time-coordinates are, the meaning of space-like simultaneous events, etc etc ... and this is a no go in this forum. No wonder you battle to grasp the essence of SR...)

 

[ghwellsjr]

...The aging rate is another word for time dilation and is not observable or measurable by either of the persons or anyone else that might be involved in the scenario...

I think this is questionable. One might think that through a little more carefully. You seem to be bringing philosophy into the mix (which I know you typically resent). By your apparent reasoning it would seem that no kind of observation or measurement is possible.

How can you say that? I also just said:

But you don't need to analyze scenarios like this using Special Relativity. You can do it simply with a Relativistic Doppler Analysis which shows physically what each person actually observes and measures. But you have to discipline yourself and not ask about physical causes beyond what can actually be measured and observed so I doubt that that would be satisfying to you either.

 

[ghwellsjr]

The aging rate is another word for time dilation and is not observable or measurable by either of the persons or anyone else that might be involved in the scenario.

Time dilation not observable? Where do you get this? This is simply wrong.
In another thread I recently tried to explain and show you that time dilation is due to relativity of simultaneity.
https://www.physicsforums.com/showpost.php?p=4189092&postcount=38
The reason you do not understand this is probably because you are too much stuck to your calculator. (And I'm afraid at the end we will have to discuss what time-coordinates are, the meaning of space-like simultaneous events, etc etc ... and this is a no go in this forum. No wonder you battle to grasp the essence of SR...)

And as I pointed out in that other thread, each of the IRF's that I drew in post #9 of this thread shows a different set of time-coordinates (and space coordinates) for each event which is illustrating the relativity of simultaneity. It also shows the relativity of time dilation. Neither of these are observable or measurable by the observers in the scenario, just like the one-way speed of light is not measurable. All three of these things are assigned by the definitions used in Special Relativity and after you assign them, then you can use the definitions and assignments to "read back" the same values you arbitrarily assigned to the events.

The essence of SR is that time is relative to the coordinate system or reference frame that you arbitrarily select. So is space. So is time dilation. So is simultaneity. Select a different coordinate system and all these characteristics change to different values. But what doesn't change are all the measurements and observations that each observer in the scenario makes. Each coordinate system preserves those measurements and observations. Maybe another way to say this is that the measurements and observations made at each event remain the same, even though the coordinates of each event take on different values in each reference frame.

 

[Vandam]

And as I pointed out in that other thread, each of the IRF's that I drew in post #9 of this thread shows a different set of time-coordinates (and space coordinates) for each event which is illustrating the relativity of simultaneity. It also shows the relativity of time dilation. Neither of these are observable or measurable by the observers in the scenario, just like the one-way speed of light is not measurable. All three of these things are assigned by the definitions used in Special Relativity and after you assign them, then you can use the definitions and assignments to "read back" the same values you arbitrarily assigned to the events.

The essence of SR is that time is relative to the coordinate system or reference frame that you arbitrarily select. So is space. So is time dilation. So is simultaneity. Select a different coordinate system and all these characteristics change to different values. But what doesn't change are all the measurements and observations that each observer in the scenario makes. Each coordinate system preserves those measurements and observations. Maybe another way to say this is that the measurements and observations made at each event remain the same, even though the coordinates of each event take on different values in each reference frame.

Maybe you draw what you observe, measure, data, and I draw in my sketches why you observe and measure what you observe... (but if I understood you elsewhere, you seem not that much interested in what lays at the origin of the observations...?).
Let me put it to you this way. Say you have a forest full of trees... You can give me thousands of different coordinate systems with enless data lists of observations, from all over the place, and all plotted out in a different diagram. But as long as you do not tell me about the forest itself, I do not get it. This is what happens in SR discussions: data list talks. And where's the forest? (I'm glad that at least Bobc2 knows what the forest is in SR... and names it: 4D block universe)

 

[PeterDonis]

Igeodesic is a mathematical term which isn't very useful to the experimenter or engineer. In terms of kinematics (i.e., without physical interaction), there is no reason that the twin on Earth has to one a geodesic everywhere. What I meant by "physical" is a local measurement that can determine where the path is not geodesic.

I already gave such a local measurement: the reading on an accelerometer. Zero acceleration measured = moving on a geodesic.

Your comment about the accelerometer is very pertinent. I believe that you have proven my point. What breaks the symmetry is a type of acceleration, just as I said. However, it can't be any type of acceleration. A kinematic acceleration, meaning an acceleration not associated with an interaction, can't break the symmetry.

A "kinematic acceleration" is not the same as acceleration measured by an accelerometer, so yes, I think I agree.

The physical quantity that determines where the path is not geodesic is whatever the accelerometer is measuring. I submit that the accelerometer is measuring the total force on the accelerometer applied by the surroundings.

This is one way of looking at it, yes.

The accelerometer is measuring the external force on it by other particles. The observer who is close to the accelerometer and stationary relative to the accelerometer is also under the influence of a force. There may be an accelerometer that is stationary and close to the observer on earth. That accelerometer does not detect an external force.

Huh? Any accelerometer at rest on the surface of the Earth will give a nonzero reading.

The quantity that the accelerometer is measuring is what I call the dynamic acceleration. I haven't found a reference that uses that phrase.

The standard term in relativity is "proper acceleration", although many texts just use "acceleration", and that's what they usually mean by it if there is no further qualification.

However, I do see scientists refer to the external force. I think the external force is what breaks the symmetry in the twin paradox. The external force usually stated in the twin paradox is caused by the rockets.

In the standard twin paradox, where one twin has to fire rockets to turn around, yes, the force generated by the rockets, which causes the traveling twin to feel acceleration, read a nonzero reading on his accelerometer, etc., is what breaks the symmetry. However, as I noted in other posts, in curved spacetime (unlike flat spacetime, which is what the standard twin paradox is set in), one can have scenarios where both twins are moving on geodesics the whole time, i.e., they never feel any acceleration, but still they age differently. So "external force breaks the symmetry" won't work in all cases.

 

[PeterDonis]

But if there are no rockets firing, it's not the rockets that are causing the difference, which Darwin123 was claiming and I was refuting. And it's not the transmission of the information that causes the difference either - it's the choosing to follow a different route to get to the same point that results in the journeys having different lengths (or different intervals, in SR language).

If there are no rockets firing, then whatever it is that is following the "different route", it can't be the traveling twin, or indeed any single object. The only word I can come up with for whatever it is that does follow the different route is "information". Perhaps that's not the best word, but we have to have some word for whatever it is that picks out the "route in spacetime" whose length is to be evaluated, in cases where no single object follows that route.

 

[Ibix]

If there are no rockets firing, then whatever it is that is following the "different route", it can't be the traveling twin, or indeed any single object. The only word I can come up with for whatever it is that does follow the different route is "information". Perhaps that's not the best word, but we have to have some word for whatever it is that picks out the "route in spacetime" whose length is to be evaluated, in cases where no single object follows that route.

I don't disagree with this. I am just trying to argue that it is the whole route that matters, not just the corners. Darwin123 seems to me to be arguing the converse.

Perhaps I need a different example. Consider twins at rest at a space station. They leave together in identical rockets at velocity +v. At time t₁, one twin fires his motors and turns round, returning to the space station at velocity -v before braking to a relative stop. The other twin carries on until time t₂, when he also turns around and returns at -v before stopping at the space station. Both twins do identical accelerations, but it's easy to show that the difference in ages when they meet up is \Delta t=2(t_2-t_1)(1-1/\gamma), which is zero only if they turn around at the same time or they don't travel at all. So acceleration isn't the only thing that matters. Both the amount of time between accelerations and the accelerations matter.

In the limited context of the classic twin paradox, you only need to know which twin accelerated to determine everything. So in this narrow circumstance, I agree one could argue that acceleration is the key. However, this isn't a useful view in general. In general, you need the complete history of both twins - i.e., their routes through spacetime.

Acceleration (or at least a frame change) is necessary for the worldlines to cross again. But it doesn't cause the age difference, any more than corners cause the triangle inequality. Different paths through a spacetime with a Minkowski geometry causes that.

 

[ghwellsjr]

And as I pointed out in that other thread, each of the IRF's that I drew in post #9 of this thread shows a different set of time-coordinates (and space coordinates) for each event which is illustrating the relativity of simultaneity. It also shows the relativity of time dilation. Neither of these are observable or measurable by the observers in the scenario, just like the one-way speed of light is not measurable. All three of these things are assigned by the definitions used in Special Relativity and after you assign them, then you can use the definitions and assignments to "read back" the same values you arbitrarily assigned to the events.

The essence of SR is that time is relative to the coordinate system or reference frame that you arbitrarily select. So is space. So is time dilation. So is simultaneity. Select a different coordinate system and all these characteristics change to different values. But what doesn't change are all the measurements and observations that each observer in the scenario makes. Each coordinate system preserves those measurements and observations. Maybe another way to say this is that the measurements and observations made at each event remain the same, even though the coordinates of each event take on different values in each reference frame.

Maybe you draw what you observe, measure, data, and I draw in my sketches why you observe and measure what you observe... (but if I understood you elsewhere, you seem not that much interested in what lays at the origin of the observations...?).
Let me put it to you this way. Say you have a forest full of trees... You can give me thousands of different coordinate systems with enless data lists of observations, from all over the place, and all plotted out in a different diagram. But as long as you do not tell me about the forest itself, I do not get it. This is what happens in SR discussions: data list talks. And where's the forest? (I'm glad that at least Bobc2 knows what the forest is in SR... and names it: 4D block universe)

Without a theory such as Special Relativity, it would be impossible to draw the data that we collect from our observations and measurements. All we would have are the lists of data. It would be and was very confusing until Einstein came along and presented his "simple and consistent theory" as he called it in the introduction of his 1905 paper.

So when I made the three separate diagrams in post #9, I used the same list of data from all observations and measurements with the aid of Einstein's definitions of what an Inertial Reference Frame (IRF) is. So the coordinates of each IRF are not part of the observations and measurements and the relationship between the coordinates and the measurements/observations are not recognizable to the observers. As I keep saying, how could they be? They change each time I use the Lorentz Transformation process to generate a new IRF and draw all the events with the new coordinate system.

You are right, I'm not interested in your opinion of "what lays at the origin of the observations" because I don't believe you or anyone else knows. In fact, I get the impression that you are promoting an idea that claims that it is no longer relative, once you see the forest for the trees. In any case, I have tried to understand the block universe concept that bobc2 and you are so fond of, but I find it so complicated that my eyes glaze over every time I see another one of those posts like #6 in the thread you linked to earlier. My opinion is that my diagrams and explanations would be easier for a newby to understand than the diagrams and explanations promoting the block universe. But, like I said in that other thread, we will have to get some feedback from various newbies to settle that issue.

In any case, I don't post comments about bobc2's or your diagrams saying that my way is "far more correct" or that there is "a danger of misinterpreting his diagrams" or implying that they are inherently incorrect or misleading. How would I know? I can't understand them.

 

[PeterDonis]

I don't disagree with this. I am just trying to argue that it is the whole route that matters, not just the corners. Darwin123 seems to me to be arguing the converse.

I think you're both right. You're right that the "corner" taken by itself is not sufficient to account for the actual differential aging that's observed; you need to look at the whole route, and by idealizing the "corner" to be instantaneous, you can idealize away any aging that actually occurs at the "corner", so that all of the actual aging has to be found by adding up aging over the segments of the route.

However, Darwin123 is right that except for the "corner", all motion involved is geodesic; so the "corner" is where you need to look if you want to find out why the "change in geodesics" occurred.

Similar remarks apply to the other scenarios you give: you have to look at the entire path through spacetime that each twin takes to get a final answer on relative aging, but if you want to understand why the paths are "crooked", why they're composed of segments of different geodesics instead of just one geodesic all the way, you need to look at the corners since that's where the "change in geodesics" happens.

 

[Vandam]

My opinion is that my diagrams and explanations would be easier for a newby to understand than the diagrams and explanations promoting the block universe.

Maybe it's enough to tell a newby that an observer sees a moving clock tick slower. And vice versa.
Everything is said by that.
Your time coordinates do not give any additional 'explanation' to it. But Block universe does.
Of course if you are not interestand in explanations then you have not to worry about that.

But I was worried about that when I came accros SR... I had to to understand the observations and maths. But again, if you are just happy putting numbers in Lorentz Tranformations... so be it.

 

[ghwellsjr]

My opinion is that my diagrams and explanations would be easier for a newby to understand than the diagrams and explanations promoting the block universe.

Maybe it's enough to tell a newby that an observer sees a moving clock tick slower. And vice versa.
Everything is said by that.

When did I ever say that? Don't you read what I write? I keep saying that an observer cannot see time dilation. I keep saying that an observer may see a moving clock ticking slower or faster than his own depending on the direction and orientation of their relative motion. I keep saying that Relativistic Doppler describes what observers see of moving clocks, not time dilation which is dependent on the selected Inertial Reference Frame (IRF) and always assigns the tick rate of moving clocks to be slower than the coordinate tick rate.

Your time coordinates do not give any additional 'explanation' to it.

They're not my time coordinates, they're Einstein's and that's what this forum is commited to teaching and helping newbies understand which is what I'm trying to do.

But Block universe does.

Like I said, I don't understand the block universe but if it promotes or teaches something that is at odds with SR, then it is not allowed here and I wouldn't be interested in it for that reason.

Of course if you are not interestand in explanations then you have not to worry about that.

But I was worried about that when I came accros SR... I had to to understand the observations and maths. But again, if you are just happy putting numbers in Lorentz Tranformations... so be it.

Yes, I find it fascinating that Einstein's concept of SR and using the Lorentz Transformation to understand relativity works the way it does. It's so simple once you understand it. I find that the biggest hurdle to helping newbies understand SR is getting rid of all the false notions they pick up from other sources, probably from those who don't understand SR themselves.

 

[bobc2]

How can you say that? I also just said:

But you don't need to analyze scenarios like this using Special Relativity. You can do it simply with a Relativistic Doppler Analysis which shows physically what each person actually observes and measures. But you have to discipline yourself and not ask about physical causes beyond what can actually be measured and observed so I doubt that that would be satisfying to you either.

That is an attitude generated back in the old Vienna Circle of philosophers, mathematicians and QM physicists. There are measurements and there are derivations. Most of our knowledge of physics is derived. Mostly, measurements performed do not directly measure the final quantity for which a "measurement" is said to have been made. The final "measurement" value is far more often than not a derived value. The speed of light was not directly measured. It was derived from measurements of distance and time. The masses of the elementary particles are not measured directly by a long shot. At NASA we used to measure the centripetal force applied to payloads under test by measuring the RPM of the centrifuge. When we measure voltage with a meter (with dial pointer) we are more directly measuring an angle of rotation of the pointer--beyond that the magnetic field strength associated with the meter movement coil, etc... Then we derive the voltage.

We could have a long discussion about examples of direct measurement of quantities in physics versus derived quanties. So, I think one has to be careful about minimizing the significance of derived "measurements" in physics. I think you make way too big a deal about the derived quanties leading to fundamental concepts in special relativity.

I don't understand your difficulty in interpreting Vandam's Loedel sketches. Many of my undergraduate students had a little trouble at first but caught on after spending some time really thinking about it. (No, I did not push block universe on them, but we did have interesting class discussions about some of the implications)

I'm really not trying to push the block universe concept here. However, I've documented in other threads the many notable physicists who embrace the concept (Paul Davies's book "About Time" is a good reference on the subject). You should not look upon it as a separate theory. It is a direct manifestation of Minkowski's geometric picture, i.e., Space-Time. Some people reject it, thinking it is a philosophical outlook. It is not. On the contrary, folks who reject it are doing it after they themselves bring in the field of philosophy--they are actually rejecting it on a philosophical basis, probably because they don't like some of the implications.

The implications--those are the cause of my own struggle with the concept. On the one hand I can't deny what Minkowski's Space-Time is showing us quite directly, but on the other hand I cannot quite make peace with it at a subjective level. I have too strong of a psychological sense of existing in a 3-D world that evolves with time. And I must give the disclaimer that I am a serious Christian and think a lot about the theological implications of foundational physics in that context.

So, my problem is that on the one hand I cannot refute the picture of the physical block universe that is manifest in special relativity, but on the other hand I can't handle it at the subjective level.

Vandam seems to have overcome those kinds of concerns--he just sticks to the facts and let's the chips fall where they may. So, for him the block universe is physical reality. (hope I haven't misrepresented Vandam). I always appreciate his comments and Loedel diagrams.

 

[ghwellsjr]

How can you say that? I also just said:

But you don't need to analyze scenarios like this using Special Relativity. You can do it simply with a Relativistic Doppler Analysis which shows physically what each person actually observes and measures. But you have to discipline yourself and not ask about physical causes beyond what can actually be measured and observed so I doubt that that would be satisfying to you either.

That is an attitude generated back in the old Vienna Circle of philosophers, mathematicians and QM physicists. There are measurements and there are derivations. Most of our knowledge of physics is derived. Mostly, measurements performed do not directly measure the final quantity for which a "measurement" is said to have been made. The final "measurement" value is far more often than not a derived value. The speed of light was not directly measured. It was derived from measurements of distance and time. The masses of the elementary particles are not measured directly by a long shot. At NASA we used to measure the centripetal force applied to payloads under test by measuring the RPM of the centrifuge. When we measure voltage with a meter (with dial pointer) we are more directly measuring an angle of rotation of the pointer--beyond that the magnetic field strength associated with the meter movement coil, etc... Then we derive the voltage.

We could have a long discussion about examples of direct measurement of quantities in physics versus derived quanties. So, I think one has to be careful about minimizing the significance of derived "measurements" in physics. I think you make way too big a deal about the derived quanties leading to fundamental concepts in special relativity.

How can you say that? I have on numerous occasions pointed out how to measure the round-trip speed of light using a single timing device colocated with a light source and a mirror some measured distance away. The determination of the speed of light is double the measured distance by the measured time interval.

But the unmeasurable one-way speed of light is defined in any Inertial Reference Frame to be equal to the measurable round trip speed of light.

But there is no way to measure or observe the time dilation of any clock. If you think there is then please describe how you would propose doing it.

For example, let's say you are moving in an IRF at some high speed. Your clock is time dilated but you can't tell, can you?

Or let's say you are observing a distant moving clock. All you can observe is the Relativistic Doppler shift which is independent of any reference frame but the propagation time of the image of the clock coming to you is dependent on the reference frame as well as the time dilation. Different frames trade off these two factors in such a way that the observation remains the same so you cannot observe or measure this trade off without which you cannot determine the time dilation. And unless you actually know what the distant clock is doing at any particular time, you can't even say what its speed is until the image of it gets to you.

I don't understand your difficulty in interpreting Vandam's Loedel sketches. Many of my undergraduate students had a little trouble at first but caught on after spending some time really thinking about it. (No, I did not push block universe on them, but we did have interesting class discussions about some of the implications)

I'm really not trying to push the block universe concept here. However, I've documented in other threads the many notable physicists who embrace the concept (Paul Davies's book "About Time" is a good reference on the subject). You should not look upon it as a separate theory. It is a direct manifestation of Minkowski's geometric picture, i.e., Space-Time. Some people reject it, thinking it is a philosophical outlook. It is not. On the contrary, folks who reject it are doing it after they themselves bring in the field of philosophy--they are actually rejecting it on a philosophical basis, probably because they don't like some of the implications.

The implications--those are the cause of my own struggle with the concept. On the one hand I can't deny what Minkowski's Space-Time is showing us quite directly, but on the other hand I cannot quite make peace with it at a subjective level. I have too strong of a psychological sense of existing in a 3-D world that evolves with time. And I must give the disclaimer that I am a serious Christian and think a lot about the theological implications of foundational physics in that context.

So, my problem is that on the one hand I cannot refute the picture of the physical block universe that is manifest in special relativity, but on the other hand I can't handle it at the subjective level.

Vandam seems to have overcome those kinds of concerns--he just sticks to the facts and let's the chips fall where they may. So, for him the block universe is physical reality. (hope I haven't misrepresented Vandam). I always appreciate his comments and Loedel diagrams.

Vandam's and your diagrams always put multiple coordinate systems into the same graph which makes it very difficult for me and I expect for a newby to grasp what is going on.

Look, as I said before, I don't complain that what you and Vandam are doing is wrong when you are presenting your explanations. Sometimes I have asked for clarification and understanding but I let you carry on without any hindrance from me. You just shouldn't complain about my explanations or insinuate that they are not accurate or not complete (unless you think they are in which case it would be helpful to specify exactly what the problem is).

 

[Vandam]

But there is no way to measure or observe the time dilation of any clock.

Again, how can you say you can not observe time dilation? Where do you get this?
I think we have to have a little converstion on what we both mean by 'observation'.

If you think there is then please describe how you would propose doing it.

Every time I or Bob gave you an explantion you tell me you do not understand it...

For example, let's say you are moving in an IRF at some high speed.

You never move in your IRF. Never.

Your clock is time dilated but you can't tell, can you?

In your own IRF your own time is never time dilated.
You do not understand relativity of simultaneity; that's the origin of time dilation!

Or let's say you are observing a distant moving clock. All you can observe is the Relativistic Doppler shift

I do not need Doppler shift to explain time dilation. Relativity of simultaneity suffices.

which is independent of any reference frame but the propagation time of the image of the clock coming to you is dependent on the reference frame as well as the time dilation. Different frames trade off these two factors in such a way that the observation remains the same so you cannot observe or measure this trade off without which you cannot determine the time dilation. And unless you actually know what the distant clock is doing at any particular time, you can't even say what its speed is until the image of it gets to you.

Vandam's and your diagrams always put multiple coordinate systems into the same graph which makes it very difficult for me and I expect for a newby to grasp what is going on.

Look, as I said before, I don't complain that what you and Vandam are doing is wrong when you are presenting your explanations. Sometimes I have asked for clarification and understanding but I let you carry on without any hindrance from me. You just shouldn't complain about my explanations or insinuate that they are not accurate or not complete
(unless you think they are in which case it would be helpful to specify exactly what the problem is).

I think we might disagree with what you mean with 'time-coordinates'. And you probably confuse 'time-coordinates' with the observation of 'observer independent clock indications'. I'll try to elaborate on this in a post sometime, when time allows me.

 

[ghwellsjr]

Vandam, I'm going to let others respond to your post. You obviously aren't going to accept anything I say. Maybe bobc2 can straighten you out since you seem to hold him in high esteem.

 

[Vandam]

You are right, I'm not interested in your opinion of "what lays at the origin of the observations" because I don't believe you or anyone else knows.

Ghwellsjr, I think you contradict yourself. Correct me if I am wrong.
SR talks about observers/observations. In order to understand SR we have to agree what observations mean, otherwise it is pointless to start dealing with observers and observations, or SR at all.
Just to make sure we understand each other as far as 'observation' is concerned;

You 'observe' (see) that an observer in the train sees a lightning hitting the front of the train because first there was lightning, then light travels to the observer, and then the light hits the observer's retinae. This is the meaning of 'to observe'. You see lightning hitting the front of the train because there is an observer independent event that's later observed by you (and other observers). There has/have to be event(s) to be observed and measured. Basic stuff. I guess you accept this.
Why then are you not interested in "what lays at the origin of the observations", i.e. the -observer independent- event: lightning hitting the front of the train?
You tell us about observation of events, but you refuse to tak about the events... Don't you contradict yourself?

SR is about observer independent events, which means: there are events out there (not part of your mind, be it physical -or mental, whatever) even before you observe them, otherwise there simply can not be an observation, nor observers.
If you refute this, then what are observations and observers in SR?

 

[ghwellsjr]

Vandam, I don't understand why you are asking me these questions when I have already specifically addressed these issues on this thread. Why don't my previous answers satisfy you?

The issue you and I are dealing with on this thread is whether or not time dilation can be observed and measured. I have said over and over again that it is dependent on the arbitrary frame of reference that you use to describe the scenario so how can it be measured by the observers in the scenario? Please go back and study my post #9 on this thread with regard to time dilation and tell me what observations or measurements the two observers can make that will enable them to determine the time dilations during each phase of the scenario and for each IRF.

 

[Vandam]

Really amazing, Ghwellsjr. Really.

 

[bobc2]

...The issue you and I are dealing with on this thread is whether or not time dilation can be observed and measured. I have said over and over again that it is dependent on the arbitrary frame of reference that you use to describe the scenario so how can it be measured by the observers in the scenario?...

ghwellsjr, I'm really not trying to be advesarial but am trying to understand your logic. Maybe we have a problem in the way we regard hyperplanes of simultaneity. Maybe if you could explain what significance you attach to this concept I would have a little better idea where you are coming from. Thanks.

 

[ghwellsjr]

...The issue you and I are dealing with on this thread is whether or not time dilation can be observed and measured. I have said over and over again that it is dependent on the arbitrary frame of reference that you use to describe the scenario so how can it be measured by the observers in the scenario?...

ghwellsjr, I'm really not trying to be advesarial but am trying to understand your logic. Maybe we have a problem in the way we regard hyperplanes of simultaneity. Maybe if you could explain what significance you attach to this concept I would have a little better idea where you are coming from. Thanks.

I have never used the term "hyperplanes of simultaneity" so now I guess I have to try to figure out what you mean by the term. If you go back to post #9 and look at the three graphs representing three different IRF's, each one of them is showing just one spatial dimension because, as is common in spacetime diagrams, we use the other dimension for time and we limit the activity in the scenario to just one dimension (usually referred to as the x-dimension) and we assume that the audience is familiar enough with this type of diagram that they know that the y- and z-dimensions are not shown but since nothing is happening at locations other than y=0 and z=0, we mentally recognize that when the graph shows a horizontal grid line, that is a line of simultaneity for a particular value of time which you look up at the left side of the graph and it means that all events along that horizontal line are simultaneous meaning they happen at the same time in that IRF. (I can't believe I'm explaining all this--nevertheless, I carry on.) Now since we don't show the y- and z- dimensions, we mentally realize that all the events that are simultaneous along that line are extrapolated out in those two extra dimensions so it is really a volume of simultaneity which I suppose is identical to your term hyperplane of simultaneity.

Now what's important is that two (or more) events that are simultaneous in one IRF (because they have the same value for their time coordinate) may not be simultaneous in another IRF as can be seen if you look at the three different graphs. I never really stopped to think in terms of a volume of simultaneity, assuming that that is what you mean by a hyperplane of simultaneity, but it is obviously the case although I would say it is so obvious that it doesn't need to be said.

Now if we wanted to show a two-dimensional scenario where the observers were moving around in both the x- and y-dimensions, we'd have a hard time putting that on a piece of paper but what we could do with today's technology is make an animation and present it as a movie. Each frame of the movie marks out a plane of simultaneity but the assumption is that it extends out into the z-dimension and so there really is a volume of simultaneity.

Does that communicate? Does it make sense to you? Is it in agreement with your concept of the hyperplane of simultaneity?

 

[bobc2]

ghwellsjr: I have never used the term "hyperplanes of simultaneity" so now I guess I have to try to figure out what you mean by the term. If you go back to post #9 and look at the three graphs representing three different IRF's, each one of them is showing just one spatial dimension because, as is common in spacetime diagrams, we use the other dimension for time and we limit the activity in the scenario to just one dimension (usually referred to as the x-dimension) and we assume that the audience is familiar enough with this type of diagram that they know that the y- and z-dimensions are not shown but since nothing is happening at locations other than y=0 and z=0, we mentally recognize that when the graph shows a horizontal grid line, that is a line of simultaneity for a particular value of time which you look up at the left side of the graph and it means that all events along that horizontal line are simultaneous meaning they happen at the same time in that IRF. (I can't believe I'm explaining all this--nevertheless, I carry on.) Now since we don't show the y- and z- dimensions, we mentally realize that all the events that are simultaneous along that line are extrapolated out in those two extra dimensions so it is really a volume of simultaneity which I suppose is identical to your term hyperplane of simultaneity.

Bobc2: Yes, we are on the same page here. Actually you do find the term “hyperplanes of simultaneity" in many places in the special relativity literature—and you have correctly figured out its meaning. I’m glad we have no problem reducing the analysis to the use of just two dimensions in our sketches.

ghwellsjr: Now what's important is that two (or more) events that are simultaneous in one IRF (because they have the same value for their time coordinate) may not be simultaneous in another IRF as can be seen if you look at the three different graphs. I never really stopped to think in terms of a volume of simultaneity, assuming that that is what you mean by a hyperplane of simultaneity, but it is obviously the case although I would say it is so obvious that it doesn't need to be said.

Bobc2: Yes, we are in perfect agreement on that. And when I use the term "hyperplanes of simultaneity" I also don't see a need to show all dimensions in the space-time diagrams.

ghwellsjr: Now if we wanted to show a two-dimensional scenario where the observers were moving around in both the x- and y-dimensions, we'd have a hard time putting that on a piece of paper…

Bobc2: But, that’s just what I’ve been trying to do with the space-time diagrams that include the various X1 axes for the different observers as well as the X4 axes. These axes are of course all identified using the velocities of the moving observers along with the Lorentz transformation. (see my first sketch below)

ghwellsjr: …but what we could do with today's technology is make an animation and present it as a movie. Each frame of the movie marks out a plane of simultaneity but the assumption is that it extends out into the z-dimension and so there really is a volume of simultaneity. Does that communicate? Does it make sense to you? Is it in agreement with your concept of the hyperplane of simultaneity?.

Bobc2: Yes, it certainly does. I have among my special relativity computer files examples of such an animation. And I’ve seen one posted on our forum here.

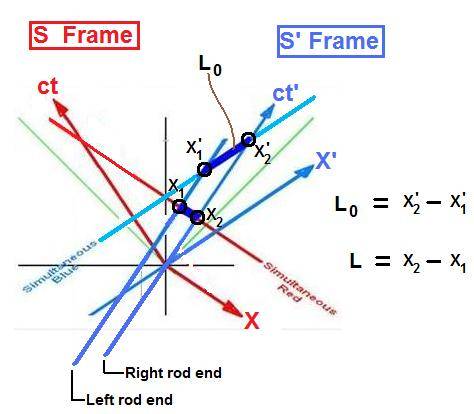
So, the sketch below illustrates how I show two different hyperplanes of simultaneity, blue and red, where two different observers are moving at the same speed in opposite directions with respect to the black inertial reference frame (the perpendicular coordinates representing X1 and X4 axes).

I have included the representation of a rod moving to the right with respect to the black frame, but the rod is at rest in the blue inertial frame. Thus, we see directly the length contraction aspect of special relativity. Blue sees the length of the rod as L0, whereas Red sees the rod length as L. And the reason I've used the symmetric space-time diagram (first introduced by Loedel of Mexico who received Einstein's blessing during their visit), is that it avoids the need to worry about the meaning of the line distances when comparing Blue and Red coordinates (you don't really need to be concerned with the hyperbolic calibration curves). This scheme was introduced to me in my first grad school special relativity course. My prof was fond of this means of communicating special relativity. I used it also later on when I was a physics instructor for undergrad physics and engineering students.

Of course it is easy to account for both X1 and X4 coordinates of Blue and Red using the Lorentz transformation hyperbolic calibration curves as shown below (the Red and Blue colors are reversed from the above sketch).

I was just trying to see if we are on the same page about the significance of these two different 3-D worlds (represented within the 4-dimensional space with just two coordinates) that blue and red occupy at points along their respective worldlines.

Finally, here is an interesting sketch, using the above concepts of hyperplanes of simultaneity to illustrate the motivation for the Block Universe model of special relativity. For now, I will spare you the pain of the addition of world lines of many different laser pulses (idealized in the diagrams as single photons). So, there is a scheme for deciphering the many laser light measurements that could be performed on signals transmitting back and forth and intersecting along the different world lines. To make the measurements more convincing you just add more observers at rest in the Blue inertial frame (collaborating results with any amount of data desired), and have matching Red observers participating in the experiment.

Perhaps I have not communicated these concepts well, or perhaps you understand the concept quite well and simply reject it. I just wanted to make sure I understood your thinking on these hyperplanes of simultaneity (X2 and X3 coordinates suppressed for clarity)
Maybe my basic questions are:

1) Do you accept the validity of the above sketches as correctly representing key aspects of special relativity (regardless of whether you attach any physical significance to it)?

2) Do you attach any physical significance to these hyperplanes of simultaneity?

3) What significance at all to the hyperplanes of simultaneity represented in the above space-time diagrams.