Boxiom
- 7
- 0
Hello!
I'm stuck at the moment with this differential equation. I've been trying to use the method for solving these equations, but my answer is not correct according to my book. Could anyone please explain what I'm doing wrong? Thanks!
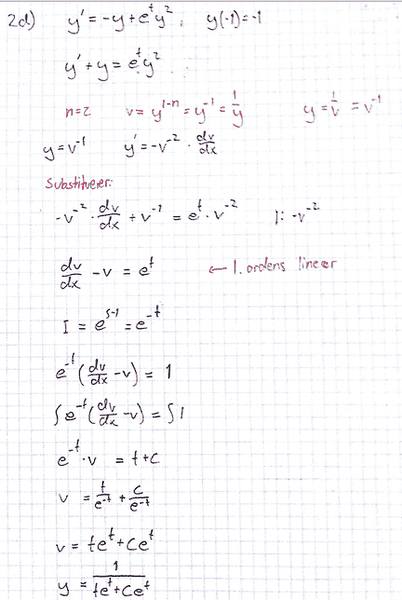
I'm stuck at the moment with this differential equation. I've been trying to use the method for solving these equations, but my answer is not correct according to my book. Could anyone please explain what I'm doing wrong? Thanks!