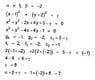Saitama
- 4,244
- 93
Homework Statement
A variable line ax+by+c=0, where a,b,c are in A.P (arithmetic progression), is normal to a circle ##(x-\alpha)^2+(y-\beta)^2=\gamma##, which is orthogonal to circle ##x^2+y^2-4x-4y-1=0##. The value of ##\alpha+\beta+\gamma## is equal to
A)3
B)5
C)10
D)7
Homework Equations
Condition for orthogonality of two circle: ##2g_1g_2+2f_1f_2=c_1+c_2##
The Attempt at a Solution
From the above condition for orthogonality: ##4\alpha+4\beta=\alpha^2+\beta^2-\gamma-1##
Since the line is normal to the circle, it passes through the centre of circle i.e. ##a\alpha+b\beta+c=0##. What should I do next?
I have 2b=a+c but where should I use this?
Any help is appreciated. Thanks!