Homework Help Overview
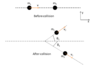
The problem involves an elastic collision between two particles of different masses, where one particle is initially stationary. The objective is to determine the maximum deviation angle of the moving particle after the collision. The context is rooted in concepts of momentum and energy conservation in physics.
Discussion Character
Approaches and Questions Raised
- Participants discuss the nature of the collision, suggesting it may be a glancing collision rather than a head-on impact. There are attempts to apply conservation laws for momentum and energy, with various equations being derived and manipulated. Some participants express confusion about the geometry involved and the implications of the angles in the collision.
Discussion Status
The discussion is ongoing, with multiple participants exploring different approaches to the problem. Some have provided guidance on using vector analysis, while others are questioning the validity of certain algebraic manipulations. There is no explicit consensus on the best method to proceed, but productive dialogue is occurring.
Contextual Notes
There are indications of confusion regarding the assumptions about the collision type and the implications of the angles involved. Participants are also navigating the complexities of vector versus scalar approaches in their reasoning.