Saitama
- 4,244
- 93
Homework Statement
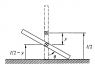
A rod of mass m and length l is held vertically on a smooth horizontal floor. If the rod begins to fall from this position, find the speed of its CM when it makes an angle ##\theta## with vertical.
Homework Equations
The Attempt at a Solution
This is a solved problem in my book and it is solved using the energy method. I was wondering if this can be solved through Newton's laws.
The forces acting on the rod are its own weight and normal reaction from the floor.
From Newton second law:
$$mg-N=ma \,\,\,\, (*)$$
Taking torque about the CM:
$$N\frac{l}{2}\sin\theta=\frac{ml^2}{12}\alpha \,\,\,\, (**)$$
where ##\alpha## is the angular acceleration about CM. Since ##\alpha=a/(l/2)##, I substitute this in (**) and solve for N. From here I get a relation between N and a. Substituting this relation in (*), I get:
$$a=\frac{3g\sin\theta}{1+3\sin\theta}$$
Since, ##a=v(dv/dy)## and ##y=l/2(1-\cos\theta)##,
$$a=2v\frac{dv}{l\sin\theta d\theta}$$
Therefore,
$$2vdv=\frac{3gl\sin^2\theta}{1+3\sin\theta}d\theta$$
The next step is to integrate both the sides. I could not integrate the right hand side so I used Wolfram Alpha.
http://www.wolframalpha.com/input/?t=crmtb01&f=ob&i=integrate sin^2(x)/(1+3sin(x)) dx
Wolfram Alpha gives a very strange answer and it does not match with the book's final answer.
Are my equations wrong?
Any help is appreciated. Thanks!