Solemony
- 6
- 0
Homework Statement
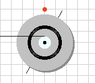
A black ring is placed concentrically on a turntable and is being pulled by a constant force of 12.5 N and the force is applied at a distance of .01m from the spindle/pulley. It's known that the ring accounts for about 8.50% of the total moment of inertia. Find moment of inertia of turntable in kg*m^2.
Note: And it's being pulled counter clockwise
Note: I have already calculated the alpha to be: 1.28 rad/s^2 (this is from data retrieved from an experiment)
Diameter of pulley :.02m (radius= .01m)
Diameter of turntable: .1m (radius = .05m)
Diameter of inner ring: .05m (radius=.025m)
Diameter of outer ring: .06m (radius= .030m)
2. Homework Equations and attempt at the problem
torque = Radius x Force
torque (pulley): .01m x 12.5N= .125N*m
torque (turntable): .05m x 12.5N = .625N*m
torque (ring): (.030m x 12.5N) - (.025m x 12.5N) = .0535N*m
So Net torque= .125+.625+.0535= .8035 N*m
Total moment of Inertia = .8035N*m/ 1.28 rad/s^2= .6277 kg*m^2
And since the ring accounts for 8.5% of the total moment of inertia I would multiply (.0850)(.6277)= .05335 kg*m^2
Then subtract .05335kg*m^2 from .6277kg*m^2 would give me the moment of inertia for the turntable?
So my question for this problem is that would I need to account the torque calculated for the turntable for the net torque? Because since the pulley/spindle is attached to the turntable and is pulled by the constant force, I would think the torque would have been just the radius of the pulley/spindle multiply by the Force (so net torque would be .125+.0535= .1785N*m instead of .8035N*m). So I wasn't sure about this part and somewhat confused as well... Thanks!
I also provided a picture for reference attached to this thread and also please point out any mistakes I've made as well if there is any calculated mistakes...