Sign Convention For v and x In Delta t = gamma(delta t' + v delta x')

[morrobay]

With Δt = γ ( Δt' + v Δx' ) For calculating delta t for stationary twin with values of traveling twin.
Is it conventional that velocity (v) outbound is positive and distance (x') is negative.
Then at turnaround point sign of velocity changes to negative. And for inbound v is negative and x' is positive ?
So outbound Δt = γ [Δ t' + v(-Δx')] At turnaround = [Δt' + (-v)(-Δx')] And inbound = [Δt' + (-v)(x')]

 

[Simon Bridge]

It's not an arbitrary convention, it depends on your coordinate system and the definition of the delta-quantities.
Go back through your notes and look for the derivation. If you don't have a derivation, do it. Work it out from first principles.

 

[morrobay]

If v= .6c to travel three light years one way , 3/3/5c = 5 years outbound + 5 years inbound from stationary twin reference. Gamma = 1.25 So in relation to above question : Δ t = γ(Δt' + vΔx')
Outbound Δ t = 1.25 [4+(.6)(-2.4)] = 3.2 yr
Turnaound point= Δt = 1.25 [ 4 + (-.6)(-2.4)] = 6.8 yr
Inbound Δt = 1.25 [ 4 + (-.6)(2.4) = 3.2yr.
So total time for stationary twin = 3.2 + 6.8 = 10 years
And 8 years for traveling twin , .8(10)

This should be correct. If the direction of velocity is closing , inbound direction, then velocity is negative. And is it correct to say here that when x is increasing its value is negative and when decreasing its value is positive ?

 

[ghwellsjr]

If v= .6c to travel three light years one way , 3/3/5c = 5 years outbound + 5 years inbound from stationary twin reference. Gamma = 1.25 So in relation to above question : Δ t = γ(Δt' + vΔx')
Outbound Δ t = 1.25 [4+(.6)(-2.4)] = 3.2 yr
Turnaound point= Δt = 1.25 [ 4 + (-.6)(-2.4)] = 6.8 yr

Where'd you get this last calculation from? It seems to me that you already calculated the turnaround point in the previous line for the Outbound Δ t.

Inbound Δt = 1.25 [ 4 + (-.6)(2.4) = 3.2yr.
So total time for stationary twin = 3.2 + 6.8 = 10 years

I don't understand why you added those two numbers together. Why wouldn't you add the Outbound Δ t to the Inbound Δt to get the total time for the stationary twin?

And 8 years for traveling twin , .8(10)

Where'd you get the factor .8 from and why did you multiply it by 10?

This should be correct. If the direction of velocity is closing , inbound direction, then velocity is negative. And is it correct to say here that when x is increasing its value is negative and when decreasing its value is positive ?

 

[Nugatory]

If v= .6c to travel three light years one way , 3/3/5c = 5 years outbound + 5 years inbound from stationary twin reference. Gamma = 1.25 So in relation to above question : Δ t = γ(Δt' + vΔx')
Outbound Δ t = 1.25 [4+(.6)(-2.4)] = 3.2 yr
Turnaound point= Δt = 1.25 [ 4 + (-.6)(-2.4)] = 6.8 yr
Inbound Δt = 1.25 [ 4 + (-.6)(2.4) = 3.2yr.
So total time for stationary twin = 3.2 + 6.8 = 10 years
And 8 years for traveling twin , .8(10)

You are confusing two different things:
1) the interval of time between events (events are things like "twins separate", "turnaround", "twins reunite", "hands of some particular clock point to noon"). These intervals are often written as $\Delta{t}$ and are related by $\Delta{t}=\gamma\Delta{t}'$.
2) the time at which a single event happens, according to some observer. If I say that a given event happens at the point $(x,t)$, an observer moving relative to me and using coordinates in which he's at rest and I'm the moving one will say that the event happened at time $t'=\gamma(t-vx)$. (Of course there's a corresponding transformation for where the event happened as well: $x'=\gamma(x-vt)$).

If the direction of velocity is closing , inbound direction, then velocity is negative. And is it correct to say here that when x is increasing its value is negative and when decreasing its value is positive ?

If the velocity vector points to the right the velocity is positive. If it points to the left, the velocity is negative. (It's worth noting that $v^2$ but not $v$ appears in $\gamma$, so the value of $\gamma$ doesn't care about the sign of $v$ but just its magnitude, and this magnitude is what we mean by "speed" or "relative speed".)

If a point lies to the right of the origin, then its $x$ value is positive. If it lies to the left of the origin, its $x$ value is negative.

All combination of $x$ positive or negative and $v$ positive or negative make sense. But do remember that different observers may be using different origins.

 

[morrobay]

Where'd you get this last calculation from? It seems to me that you already calculated the turnaround point in the previous line for the Outbound Δ t.



I don't understand why you added those two numbers together. Why wouldn't you add the Outbound Δ t to the Inbound Δt to get the total time for the stationary twin?



Where'd you get the factor .8 from and why did you multiply it by 10?

In previous line as indicated outbound time = 3.2 years. Not the same as turnaround time. If you look more closely at the + and - signs you will see they are not the same. Also note that it is these different signs on values in equation that account for turnaround time of 6.8 years

Since turnaround time , 6.8 years, succeeded outbound time then it is turnaround time that is added to inbound time , 3.2 years, = 10 years stationary observers total time

At .6 c the Lorentz factor is [1-v²/c²]^1/2 = .8
So (.8) (10) = 8 years for traveler . 4 + 4 in post #3

 

[Nugatory]

In previous line as indicated outbound time = 3.2 years. Not the same as turnaround time. If you look more closely at the + and - signs you will see they are not the same. Also note that it is these different signs on values in equation that account for turnaround time of 6.8 years

Since turnaround time , 6.8 years, succeeded outbound time then it is turnaround time that is added to inbound time , 3.2 years, = 10 years stationary observers total time

At .6 c the Lorentz factor is [1-v²/c²]^1/2 = .8
So (.8) (10) = 8 years for traveler . 4 + 4 in post #3

You might want to try repeating this calculation using frames in which the traveller is at rest, so stay-at-home is moving at $-v$ before traveler turns around and at $v$ after the turnaround.

 

[morrobay]

You are confusing two different things:
1) the interval of time between events (events are things like "twins separate", "turnaround", "twins reunite", "hands of some particular clock point to noon"). These intervals are often written as $\Delta{t}$ and are related by $\Delta{t}=\gamma\Delta{t}'$.
2) the time at which a single event happens, according to some observer. If I say that a given event happens at the point $(x,t)$, an observer moving relative to me and using coordinates in which he's at rest and I'm the moving one will say that the event happened at time $t'=\gamma(t-vx)$. (Of course there's a corresponding transformation for where the event happened as well: $x'=\gamma(x-vt)$).



If the velocity vector points to the right the velocity is positive. If it points to the left, the velocity is negative. (It's worth noting that $v^2$ but not $v$ appears in $\gamma$, so the value of $\gamma$ doesn't care about the sign of $v$ but just its magnitude, and this magnitude is what we mean by "speed" or "relative speed".)

If a point lies to the right of the origin, then its $x$ value is positive. If it lies to the left of the origin, its $x$ value is negative.

All combination of $x$ positive or negative and $v$ positive or negative make sense. But do remember that different observers may be using different origins.

Yes Δt' = Δt/γ and Δt' = γ ( Δt - vΔx) are two different things, proper time and coordinate times. However the elapsed times are equal :

If v= .6c , γ = 1.25 and Lorentz factor = .8. So with 5 years travel at .6c. Δx = 3 light-years.
Δ t' = 1.25 [ 5 - (.6)(3) ] = 4 years. And Δt' = Δt/γ = 4 years

Also note that the above values can be used for the invariant space time interval for S and S'

Δt = 5 yrs , Δx = 3 ly so √ 5²-3²...S = 4
Δt'= 4 yrs. Δx = 0 so √4²-0 ...S' = 4

 

[ghwellsjr]

Where'd you get this last calculation from? It seems to me that you already calculated the turnaround point in the previous line for the Outbound Δ t.

In previous line as indicated outbound time = 3.2 years.

Let's take a look at that previous line (in bold) and the ones before it to provide the context:

If v= .6c to travel three light years one way , 3/3/5c = 5 years outbound + 5 years inbound from stationary twin reference. Gamma = 1.25 So in relation to above question : Δ t = γ(Δt' + vΔx')
Outbound Δ t = 1.25 [4+(.6)(-2.4)] = 3.2 yr

I think I understand what you did here and I see no problem with it. Tell me if these spacetime diagrams depict your scenario and your calculation:

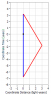
We start with the rest frame of the traveling twin shown in red as he is traveling away from the stationary twin shown in blue. His clock at the moment of turnaround is at 4 years and you want to use the simultaneous event shown as a black dot for the stationary twin. You show this as the Δt' parameter in the bolded equation for the Coordinate Time interval from the start of the trip. You calculated the Δx' parameter by multiplying the velocity, -0.6c, times the Coordinate Time of 4 years to get -2.4 light years. Here is the corresponding spacetime diagram:

Next you want to transform this to the rest frame of the stationary twin which you can do by setting the speed to 0.6c. (This is backwards from the more usual form of the LT where the speed is negative but the sign at the front of the product is also negative so it ends up being positive.) Here is the rest frame of the stationary twin with the black dot showing the value of Δt=3.2 years:

You didn't show the calculation for Δx but if you had it would have gone like this:

Δx = 1.25 [-2.4+(.6)(4)] = 0 light years. This is also correctly depicted on the diagram. I agree with what you have done so far.

Not the same as turnaround time. If you look more closely at the + and - signs you will see they are not the same. Also note that it is these different signs on values in equation that account for turnaround time of 6.8 years

Now here is where not calculating the spatial interval, I think, has gotten you into trouble. If you had it would have gone like this:

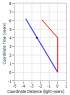
Δx = 1.25 [-2.4+(-0.6)(4)] = 1.25 [-2.4 -2.4] = 1.25 [-4.8] = -6 light years. This should also be zero for a legitimate analysis. Here is the space time diagram that you get when you transform the first diagram to the same speed but opposite direction as the second diagram:

I don't understand why you added those two numbers together. Why wouldn't you add the Outbound Δ t to the Inbound Δt to get the total time for the stationary twin?

Since turnaround time , 6.8 years, succeeded outbound time then it is turnaround time that is added to inbound time , 3.2 years, = 10 years stationary observers total time

The fact that you got the correct number, 6.8 years that you needed to add to 3.2 years to get 10 years, doesn't make it the correct calculation, at least as far as I can tell. Maybe I completely misunderstood what you were doing, in which case, you need to enlighten me.

Now if we continue on to your last calculation:

Inbound Δt = 1.25 [ 4 + (-.6)(2.4) = 3.2yr.

It appears to me that this corresponds to the rest frame of the traveling twin on his way back:

The intervals for the stationary twin that is simultaneous with the traveling twin's turnaround event are Δt' = 4 years and Δx' = 2.4 light years and the corresponding event is shown by the black dot. Transforming to a speed of 0.6c, we get:

This shows the same time interval that you calculated before of 3.2 years. If this accurately portrays what you had in mind, then I agree with this part.

However, the first and third calculations of 3.2 years don't add up to 10 years and they illustrate the famous "time gap" that occurs when the analysis has the traveling twin "jumping" frames.

Where'd you get the factor .8 from and why did you multiply it by 10?

At .6 c the Lorentz factor is [1-v²/c²]^1/2 = .8
So (.8) (10) = 8 years for traveler . 4 + 4 in post #3

Can you please provide an online reference for your definition of the Lorentz factor? Every definition I have seen equates it with gamma so it has a value of 1.25 in this post, not 0.8.

 

[morrobay]

Yes gamma = Lorentz factor , my error. I should have denoted 1/γ as Lorentz contraction.
In your second graph for stationary twin in addition to black dot at 0,3.2 there can also be a dot at 0.6.8 .
Both representing lines of simultaneity to point 3,5 for traveler. So you are questioning the
validity of how I arrived at Δt = 6.8 years at turnaround point based on your calculation of Δx= γ( Δx'+vΔt')
at turnaround point using the same signs, v = -.6 and Δx' = - 2.4
You got Δx = -6 light years and it should be Δx = 0 .
I got the correct time Δt = 6.8 yrs at turnaround point with Δt = γ ( Δt' + vΔx') using negative signs for v and Δx'.

Then this leads to this question : At the turnaround /reference frame change point is it possible
to have different signs on the v and Δx' values when calculating Δx ? Ie in order to
produce the correct value of Δx = 0.

 

[ghwellsjr]

I got the correct time Δt = 6.8 yrs at turnaround point with Δt = γ ( Δt' + vΔx') using negative signs for v and Δx'.

Then this leads to this question : At the turnaround /reference frame change point is it possible
to have different signs on the v and Δx' values when calculating Δx ? Ie in order to
produce the correct value of Δx = 0.

I'm glad you recognize the problem. I think it's possible to use a negative sign for v but not for Δx'. It's a rather long process because, if I understand your purpose, you want to use the information from the traveling twin to determine the stationary twin's total time. So here's what we have to do:

Let's go back to the original frame:

Obviously, I had to know the answer to the question of what the total time is for the stationary twin in order to draw this diagram but let's assume we don't know that and we want to let the Lorentz Transformation process determine it for us. Here's another truncated version of the diagram showing just a little progress for both twins after the turnaround time:

We used this frame to calculate the time from the beginning of the scenario (where the origin is) to the event depicted as the black dot on the stationary twin's worldline that is simultaneous with the turnaround event on the traveling twin's worldline. Then we transformed to the stationary twin's rest frame to determine how much time progressed for him from the beginning to the black dot.

Now we want to do a similar thing but starting with the black dot and going up to the reunion of the twins. So the first thing we want to do is shift the origin up to the black dot. All we have to do is add 2.4 to all the x coordinates and subtract 4 from all the time coordinates. This puts the coordinates of the turnaround event at x'=2.4 and t'=0:

Next we transform all the coordinates to a frame moving at v=0.6 and we get new coordinates for the turnaround event of x'=3 and t'=1.8:

We have to transform to another frame moving at v=0.6 to get the traveling twin's worldline to be vertical. The coordinates of the turnaround event in this frame are x'=5.1 and t'=4.5:

Now we want to move up from the traveling twin's turn around event by 4 years to the reunion event and we end up with coordinates of x'=5.1 and t'=8.5:

Finally we are ready to take the last transform, this time with v=-0.6 and we get new coordinates for the reunion event of x=0 and t=6.8 which is our desired features:

And we can extend the stationary twin's worldline by 6.8 seconds to the reunion event: