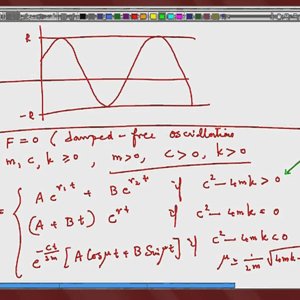
Differential eqautions Definition and 96 Threads

  1. sergiokapone

    Undergrad Integral and differential forms of field equations

    I have a question, is there some other fundamental difference in the integral and differential form of the field equations that is missed here and should have been mentioned?
    • sergiokapone
    • Thread
    • Differential eqautions field equations Integral calculus Maxwel's equations
    • Replies: 16
    • Forum: Electromagnetism
  2. PLAGUE

    Books on D Operator Method

    TL;DR Summary: Comprehensive books on D Operator method Currently I am studying (Ordinary) Differential equation but the book I am following doesn't include much on D Operator Method of solving differential equations. Please suggest me some (Ordinary Differential Equation) books that goes...
  3. ematt

    Graduate Symplectic split of Hamiltonian with complex term

    Is it possible to express symplectic split integrator for Hamiltonian containing an extra imaginary term? For instance H=T+V+iV_2
  4. Hamiltonian

    How Do You Solve a Differential Equation Using an Ansatz?

    Finding the first and second derivative of out ansatz, $$\dot x(t)=A(cos(\omega_0 t) - t\omega_0 sin(\omega_0 t)) + B(sin(\omega_0 t) + t\omega_0 cos(\omega_0 t))$$ $$\ddot x= A(-2\omega_0 sin(\omega_0 t) - t{\omega_0}^2cos(\omega_0 t)) + B(2\omega_0 cos(\omega_0 cos(\omega_0 t)...
  5. S

    High School Why doesn't the Navier-Stokes equation have a solution?

    Why the navier-stokes equation don't have a solution ?
    • Sawawdeh
    • Thread
    • Differential eqautions Hydrodynamics
    • Replies: 5
    • Forum: Mechanics
  6. Lotto

    Movement of the water level in the barrel - calculate its velocity, etc.

    Here is only my solution: ##A_1 \frac{\mathrm d h}{\mathrm d t}=-A_2\sqrt{2hg}##, so by integrating we get ##h(t)=\left(\sqrt{h_0}-\frac{A_2}{2A_1}\sqrt{2g} t\right)^2.## Setting ##h(T)=0## we get ##T=\frac{A_1}{A_2}\sqrt{\frac{2h_0}{g}}.## By doing the first time derivative of ##h## we...
  7. P

    Relativistic particle moving in a potential

    Since energy is conserved and the particle is initially at rest, we can determine that ##E(0) = m_0 c^2##, so $$ m_0 c^2 = \sqrt{ c^2 p^2 + m_0^2 c^4 } + \alpha x. $$ Squaring this eqation gives $$ m_0^2 c^4 = \alpha^2 x^2 + c^2 p^2 + m_0^2 c^4 + 2 \alpha x \sqrt{ c^2 p^2 + m_0^2 c^4 }...
  8. H

    Mathematica How to check a particular solution of System of Linear ODEs?

    If I have been given a system of inhomogeneous linear ODEs, $$ \vec{x'} = \begin{bmatrix} 4 & -1 \\ 5 & -2 \\ \end{bmatrix} \vec{x} + \begin{bmatrix} 18e^{2t} \\ 30e^{2t}\\ \end{bmatrix} $$ I have found its particular solution to be: $$ 1/4 \begin{bmatrix} -31e^{2t} - 25e^{6t} \\ 85e^{2t} -...
  9. H

    Solving ##y'' - 5 y' - 6y = e^{3x}## using Laplace Transform

    We have to solve $$ \begin{align*} y'' - 5y' - 6y = e^{3x} \\ y(0) = 2,~~ y'(0) = 1 \\ \end{align*} $$ Applying Laplace Transform the equation $$ \begin{align*} L [ y''] - 5 L[y'] - 6 L[y] = L [ e^{3x} ] \\ s^2 Y(s) - \left( s y(0) + y'(0) \right) - 5s Y(s) + y(0) - 6 Y(s) = \frac{1}{s-3} \\...
  10. hagopbul

    Undergrad Drawing Direction Fields for Higher Order ODEs

    Hello : Trying to find references on drawing direction fields of higher order differential equation by hand as 1st step then by computer , do you know any reference I can read ( PDF , books ,...) , and hope it is not only some short notes Best regards HB
  11. J

    Using the Frobenius method on a 2D Laplace

  12. L

    Prove eigenvalues of the derivatives of Legendre polynomials >= 0

    The problem has a hint about finding a relationship between ##\int_{-1}^1 (P^{(k+1)}(x))^2 f(x) dx## and ##\int_{-1}^1 (P^{(k)}(x))^2 g(x) dx## for suitable ##f, g##. It looks they're the weighting functions in the Sturm-Liouville theory and we may be able to make use of Parseval's identity...
  13. Ibidy

    Struggling to find solution to 1D wave equation in the following form:

  14. potatocake

    Is My Solution to This Exact Differential Equation Correct?

    (x cos(y) + x2 +y ) dx = - (x + y2 - (x2)/2 sin y ) dy I integrated both sides 1/2x2cos(y) + 1/3 x3+xy = -xy - 1/3y3+x2cos(y) Then I get x3 + 6xy + y3 = 0 Am I doing the calculations correctly? Do I need to solve it in another way?
  15. D

    Prerequisite mathematics for intermediate mechanics?

    I will be taking intermediate mechanics next semester, and am a bit concerned about potential gaps in my mathematical knowledge. Long story short, I used to be a physics major, switched to electrical engineering, and then decided to double major after a semester in EE. The issue is that, as a...
    • dpatnd
    • Thread
    • Differential eqautions Linear algagbra Math and physics Mathematics Mechanics Prerequisites
    • Replies: 4
    • Forum: Mechanics
  16. quantumCircuit

    Lotka Volterra estimate parameters from experimental data

    Namely, in the system, I have obtained the value of parameters L, M, A and D, because I treat the other organism as equal to zero, i.e., it doesn't exist, but I am struggling about the values of B and C, that are coupled with the product of x and y. Can anyone help me how to obtain those values...
  17. M

    Graduate Solving a differential equation with two unknowns

    One thing that is given in paper (attached) is a operating set point for temperature which is given as 20 for day and 16 for night but I do not know whether its initial condition for temperature or not. Can anyone please guide me that what kind of equation is it and how can I solve it with these...
  18. O

    Undergrad The Trapping Region of the Lorenz equations

    I was dealing with nonlinear systems of differential equations like the Lorenz equations (https://en.wikipedia.org/wiki/Lorenz_system). Now there is a trapping region of this system defined by the ellipsoid ρx^2+σy^2+σ(z-2ρ)^2<R. I wondered how this region is found and I found out that a...
  19. J

    Calculus What is the best textbook for understanding differentials?

    Hi, I am an undergrad looking to purchase a good textbook on differentials for my course which I will be taking soon, and the textbook listed for the differentials course is this one (https://www.amazon.com/gp/product/1118531779/?tag=pfamazon01-20) which apparently is not very good. So can...
  20. The Coronavirus Curve Simulation - Numberphile

    The Coronavirus Curve Simulation - Numberphile

    Ben Sparks uses https://www.GeoGebra.org to explain (and code) the so-called SIR Model being used to predict the spread of cornavirus (COVID-19). A pretty cool way to visualize a set of differential equations.
    • scottdave
    • Media item
    • Coronavirus Differential eqautions Numerical analysis
    • Comments: 1
    • Category: Differential Equations
  21. O

    How to prove this statement about the derivative of a function

    My try: ##\begin{align} \dfrac{d {r^2}}{d r} \dfrac{\partial r}{\partial p} = \dfrac{\partial {r^2}}{\partial p} \tag1\\ \dfrac{\partial r}{\partial p} = \dfrac{\partial {r^2}}{\partial p} \dfrac{1}{\dfrac{d r^2}{d r}}=\dfrac{p-a\cos\theta}{r} \tag2\\ \end{align}## By chain rule...
  22. J

    The range for y if t>=10 is [-4, 0].

    From integration by parts, and using y(10) = 0, I get the equation ##2e^{3t-30} = \frac{|y-2|}{|y+1|}.## Let ##f(t) = 2e^{3t-30}##. Since it's for t>10, f(10) = 2, and we have ##2=\frac{|y-2|}{|y+1|}##. Depending on the sign I choose to use, I get either that y=-4 or y =0. Since ##t: 10...
  23. A

    Undergrad When and How to Solve ODEs: Clarity for Confused Students

    I know how to solve ODEs using both methods. The problem I'm having is knowing when to use one and not the other. If someone could help clarify this for me. I can't find the correct section in my textbook.
  24. K

    Differential equation problem: Modeling the spread of a rumor on campus

    So this is what I have done: ##f'(t)=k*f(t)*(A-f(t))*(1-sin(\frac{pi*x}{12}))## ##\frac{1}{f(t)*(A-f(t))}=k*(1-sin(\frac{pi*x}{12}))## I see that the left can be written as this (using partial fractions): ##1/A(\frac{1}{f(t)}-\frac{1}{A-f(t)})## And then I take the integral on both sides and...
  25. aligator11

    Particle Dynamics Problem (kinematics)

    Summary: Mechanics problem related with Calculus (differential equations) Hi everyone, I would like some help in that task, if anyone would be willing to help :) Namely I have a problem from particle dynamics. "D:" means given info... so, D: m,g,h,b, miu. We're looking for v0 and S as given...
  26. christang_1023

    Solve the differential equation of motional emf

    . Above is the figure of the problem. I am trying to solve x(t) and differentiate it to obtain v(t); however, I have difficulty solving the differential equation shown below. $$ v(t)=\int a(t)dt=\int \frac{B(\varepsilon-Blv)d}{Rm}dt \Rightarrow \frac{dx}{dt}=\frac{B\varepsilon...
  27. R

    How do you solve a differential equation with complex numbers?

    Homework Statement Homework Equations euler ##e^{ix} = cos(x) + i*sin(x)## ##e^{-ix} = cos(x) - i*sin(x)## The Attempt at a Solution I'm starting with differential equations and I'm trying to understand this solution including complex numbers: First we determine the zeros. I understand that...
  28. JD_PM

    Proving that a vector field is conservative

    Homework Statement Homework Equations $$F = \nabla \phi$$ The Attempt at a Solution Let's focus on determining why this vector field is conservative. The answer is the following: [/B] I get everything till it starts playing with the constant of integration once the straightforward...
  29. B

    Undergrad Solution of the 1D heat equation

    $$\frac{\partial T}{\partial t}=\alpha\frac{\partial^2 T}{\partial^2 t}$$ with an initial condition and boundary conditions $$T(x,0)=T_0$$ $$T(L,t)=T_0$$ $$-k\left.\frac{\partial T}{\partial x}\right|_{x=0}=2A\cos^2\left(\frac{\omega t}{2}\right)=A(\cos\omega t+1)$$ where $A=V_0^2/(8RhL)$...
    • Betsy
    • Thread
    • 1d Differential eqautions Heat Heat and mass transfer Heat capacity Heat equation Thermal conductivity
    • Replies: 8
    • Forum: Differential Equations
  30. Z

    Differential Equation with an Initial condition

    Homework Statement x(dy/dx) = 3y +x4cos(x), y(2pi)=0 Homework Equations N/A The Attempt at a Solution I've tried a couple different ways to make this separable, but you always carry over a 1/dx or 1/dy term and I can never fully separate this. I've also tried to do a Bernoulli differential...
  31. T

    Graduate Determine PDE Boundary Condition via Analytical solution

    I am trying to determine an outer boundary condition for the following PDE at ##r=r_m##: $$ \frac{\sigma_I}{r} \frac{\partial}{\partial r} \left(r \frac{\partial z(r,t)}{\partial r} \right)=\rho_D gz(r,t)-p(r,t)-4 \mu_T \frac{\partial^2z(r,t)}{\partial r^2} \frac{\partial z(r,t)}{\partial t} $$...
    • tse8682
    • Thread
    • Analytical Analytical solution Bessel function Boundary Boundary condition Condition Differential eqautions Ordinary differential equation Partial differential equations Pde
    • Replies: 1
    • Forum: Differential Equations
  32. thoraxepi

    Undergrad Transfer Function relating momentum and force

    Hey all, I hope this is the correct forum section to post this in. I heard about this problem from a youtube video but I've not been able to simulate it because the video was meant only for an introduction into PID control. Here's the problem: A remote control helicopter is hovering just...
    • thoraxepi
    • Thread
    • Differential eqautions Force Function Laplace transform Momentum Process control Transfer fucntion Transfer function
    • Replies: 2
    • Forum: Differential Equations
  33. W

    Finding Orthogonal Trajectories (differential equations)

    Homework Statement Find Orthogonal Trajectories of ##\frac{x^2}{a}-\frac{y^2}{a-1}=1## Hint Substitute a new independent variable w ##x^2=w## and an new dependent variable z ##y^2=z## Homework EquationsThe Attempt at a Solution substituting ##x## and ##y## I get...
  34. Jozefina Gramatikova

    Separate the following PDE as much as possible

    Homework Statement [/B]Homework Equations [/B]The Attempt at a Solution [/B] Could you tell me is there something specific that I need to the with sin(xy)? Thanks
  35. P

    Undergrad How does the substitution x = 1/z transform Bessel's Equation?

    Hi! When we want to look at different singular points for e.g Bessel's eq. $$u´´(x) + \frac{u'(x)}{x} + (1- \frac{n^2}{x^2})u(x)$$. We usually evaluate the equation letting x= 1/z. But I don't algebraically see how such a substitution ends up with $$w´´(z) +( \frac{2}{z}-...
  36. A

    Undergrad Understanding Linearity of Differential Equations

    Hey all, I don't understand what makes a differential equation (DE) linear. I found this: "x y' = 1 is non-linear because y' is not multiplied by a constant" but then also this: "x' + (t^2)x = 0 is linear in x". t^2 also isn't a constant. So why is this equation linear?
  37. Differential Equations and Applications (NPTEL):- Lecture 01: General Introduction

    Differential Equations and Applications (NPTEL):- Lecture 01: General Introduction

    COPYRIGHT strictly reserved to A. K. Nandakumaran, P. S. Datti & Raju K. George, Department of Mathematics, IISc Bangalore. Duplication PROHIBITED. Lectures: http://www.nptel.ac.in/courses/111108081/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108081
    • Wrichik Basu
    • Media item
    • differential eqautions nptel
    • Comments: 0
    • Category: Differential Equations
  38. Differential Equations and Applications (NPTEL):- Lecture 02: Examples I

    Differential Equations and Applications (NPTEL):- Lecture 02: Examples I

    COPYRIGHT strictly reserved to A. K. Nandakumaran, P. S. Datti & Raju K. George, Department of Mathematics, IISc Bangalore. Duplication PROHIBITED. Lectures: http://www.nptel.ac.in/courses/111108081/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108081
    • Wrichik Basu
    • Media item
    • differential eqautions nptel
    • Comments: 0
    • Category: Differential Equations
  39. Differential Equations and Applications (NPTEL):- Lecture 03: Examples II

    Differential Equations and Applications (NPTEL):- Lecture 03: Examples II

    COPYRIGHT strictly reserved to A. K. Nandakumaran, P. S. Datti & Raju K. George, Department of Mathematics, IISc Bangalore. Duplication PROHIBITED. Lectures: http://www.nptel.ac.in/courses/111108081/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108081
    • Wrichik Basu
    • Media item
    • differential eqautions nptel
    • Comments: 0
    • Category: Differential Equations
  40. Differential Equations and Applications (NPTEL):- Lecture 04: Examples III

    Differential Equations and Applications (NPTEL):- Lecture 04: Examples III

    COPYRIGHT strictly reserved to A. K. Nandakumaran, P. S. Datti & Raju K. George, Department of Mathematics, IISc Bangalore. Duplication PROHIBITED. Lectures: http://www.nptel.ac.in/courses/111108081/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108081
    • Wrichik Basu
    • Media item
    • differential eqautions nptel
    • Comments: 0
    • Category: Differential Equations
  41. Differential Equations and Applications (NPTEL):- Lecture 05: Linear Algebra I

    Differential Equations and Applications (NPTEL):- Lecture 05: Linear Algebra I

    COPYRIGHT strictly reserved to A. K. Nandakumaran, P. S. Datti & Raju K. George, Department of Mathematics, IISc Bangalore. Duplication PROHIBITED. Lectures: http://www.nptel.ac.in/courses/111108081/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108081
    • Wrichik Basu
    • Media item
    • differential eqautions nptel
    • Comments: 0
    • Category: Differential Equations
  42. Differential Equations and Applications (NPTEL):- Lecture 06: Linear Algebra II

    Differential Equations and Applications (NPTEL):- Lecture 06: Linear Algebra II

    COPYRIGHT strictly reserved to A. K. Nandakumaran, P. S. Datti & Raju K. George, Department of Mathematics, IISc Bangalore. Duplication PROHIBITED. Lectures: http://www.nptel.ac.in/courses/111108081/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108081
    • Wrichik Basu
    • Media item
    • differential eqautions nptel
    • Comments: 0
    • Category: Differential Equations
  43. Differential Equations and Applications (NPTEL):- Lecture 07: Linear Algebra III

    Differential Equations and Applications (NPTEL):- Lecture 07: Linear Algebra III

    COPYRIGHT strictly reserved to A. K. Nandakumaran, P. S. Datti & Raju K. George, Department of Mathematics, IISc Bangalore. Duplication PROHIBITED. Lectures: http://www.nptel.ac.in/courses/111108081/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108081
    • Wrichik Basu
    • Media item
    • differential eqautions nptel
    • Comments: 0
    • Category: Differential Equations
  44. Differential Equations and Applications (NPTEL):- Lecture 08: Analysis I

    Differential Equations and Applications (NPTEL):- Lecture 08: Analysis I

    COPYRIGHT strictly reserved to A. K. Nandakumaran, P. S. Datti & Raju K. George, Department of Mathematics, IISc Bangalore. Duplication PROHIBITED. Lectures: http://www.nptel.ac.in/courses/111108081/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108081
    • Wrichik Basu
    • Media item
    • differential eqautions nptel
    • Comments: 0
    • Category: Differential Equations
  45. Differential Equations and Applications (NPTEL):- Lecture 09: Analysis II

    Differential Equations and Applications (NPTEL):- Lecture 09: Analysis II

    COPYRIGHT strictly reserved to A. K. Nandakumaran, P. S. Datti & Raju K. George, Department of Mathematics, IISc Bangalore. Duplication PROHIBITED. Lectures: http://www.nptel.ac.in/courses/111108081/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108081
    • Wrichik Basu
    • Media item
    • differential eqautions nptel
    • Comments: 0
    • Category: Differential Equations
  46. Differential Equations and Applications (NPTEL):- Lecture 10: First Order Linear Equations

    Differential Equations and Applications (NPTEL):- Lecture 10: First Order Linear Equations

    COPYRIGHT strictly reserved to A. K. Nandakumaran, P. S. Datti & Raju K. George, Department of Mathematics, IISc Bangalore. Duplication PROHIBITED. Lectures: http://www.nptel.ac.in/courses/111108081/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108081
    • Wrichik Basu
    • Media item
    • differential eqautions nptel
    • Comments: 0
    • Category: Differential Equations
  47. Differential Equations and Applications (NPTEL):- Lecture 11: Exact Equations

    Differential Equations and Applications (NPTEL):- Lecture 11: Exact Equations

    COPYRIGHT strictly reserved to A. K. Nandakumaran, P. S. Datti & Raju K. George, Department of Mathematics, IISc Bangalore. Duplication PROHIBITED. Lectures: http://www.nptel.ac.in/courses/111108081/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108081
    • Wrichik Basu
    • Media item
    • differential eqautions nptel
    • Comments: 0
    • Category: Differential Equations
  48. Differential Equations and Applications (NPTEL):- Lecture 12: Second Order Linear Equations I

    Differential Equations and Applications (NPTEL):- Lecture 12: Second Order Linear Equations I

    COPYRIGHT strictly reserved to A. K. Nandakumaran, P. S. Datti & Raju K. George, Department of Mathematics, IISc Bangalore. Duplication PROHIBITED. Lectures: http://www.nptel.ac.in/courses/111108081/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108081
    • Wrichik Basu
    • Media item
    • differential eqautions nptel
    • Comments: 0
    • Category: Differential Equations
  49. Differential Equations and Applications (NPTEL):- Lecture 13: Second Order Linear Equations II

    Differential Equations and Applications (NPTEL):- Lecture 13: Second Order Linear Equations II

    COPYRIGHT strictly reserved to A. K. Nandakumaran, P. S. Datti & Raju K. George, Department of Mathematics, IISc Bangalore. Duplication PROHIBITED. Lectures: http://www.nptel.ac.in/courses/111108081/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108081
    • Wrichik Basu
    • Media item
    • differential eqautions nptel
    • Comments: 0
    • Category: Differential Equations
  50. Differential Equations and Applications (NPTEL):- Lecture 14: Second Order Linear Equations III

    Differential Equations and Applications (NPTEL):- Lecture 14: Second Order Linear Equations III

    COPYRIGHT strictly reserved to A. K. Nandakumaran, P. S. Datti & Raju K. George, Department of Mathematics, IISc Bangalore. Duplication PROHIBITED. Lectures: http://www.nptel.ac.in/courses/111108081/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108081
    • Wrichik Basu
    • Media item
    • differential eqautions nptel
    • Comments: 0
    • Category: Differential Equations