Linear algebra Definition and 999 Threads
-
Courses On the benefits of retaking advanced linear algebra
I'm a physics student who has the option to take some advanced math courses (Real analysis through Rudin and beyond, functional analysis if I have time, as well as algebra through Artin). I'm only just going into my second year this term, and will either be retaking linear algebra 2, or taking...- mcabbage
- Thread
- Replies: 2
- Forum: STEM Academic Advising
-
I Confused by this result for the tensor product of two vectors
Given two probability distributions ##p \in R^{m}_{+}## and ##q \in R^{n}_{+}## (the "+" subscript simply indicates non-negative elements), this paper (page 4) writes down the tensor product as $$p \otimes q := \begin{pmatrix} p(1)q(1) \\ p(1)q(2) \\ \vdots \\ p(1)q(n) \\ \vdots \\...- Prez Cannady
- Thread
- Replies: 3
- Forum: Linear and Abstract Algebra
-
I Munkres-Analysis on Manifolds: Theorem 20.1
Hello. I am studying Analysis on Manifolds by Munkres. I have a problem with a proof in section 20. It states that: Let A be an n by n matrix. Let h:R^n->R^n be the linear transformation h(x)=A x. Let S be a rectifiable set (the boundary of S BdS has measure 0) in R^n. Then v(h(S))=|detA|v(S)...- Bill2500
- Thread
- Replies: 5
- Forum: Topology and Analysis
-
The Maximum Rank of a Matrix B Given AB=0 and A is a Full Rank Matrix
Homework Statement Suppose that AB = 0, where A is a 3 x 7 full rank matrix and B is 7 x 53. What is the highest possible rank of matrix B. Homework EquationsThe Attempt at a Solution Since each column of B is in the null space of A, the rank of B is at most 4. I don't understand why it is...- TickleTackleTock
- Thread
-
- Tags
- Algebra Linear Linear algebra rank
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
I Rotation of a point in R3 about the y-axis
Hello, I'm having a visualisation problem. I have a point in R3 that I want to rotate about the ##y##-axis anticlockwise (assuming a right-handed cartesian coordinate system.) I know that the change to the point's ##x## and ##z## coordinates can be described as follows: $$z =...- NatFex
- Thread
- Replies: 6
- Forum: Linear and Abstract Algebra
-
B
Courses Applied vs Proof Based Linear Algebra
Hi, I’m going to be entering my first year of University this fall to study physics. In my second semester I will have to take a linear algebra course; however, my school has two different lower level linear algebra courses, and I must choose one. One course is focused more on applications of...- bentleyghioda
- Thread
- Replies: 9
- Forum: STEM Academic Advising
-
Programs As a year II physics major, when should I take linear algebra
After seeing so much higher-level physics and proofing for special relativity, I imagine I'll need to take this at some point to continue do grad-level physics. I'm taking calc III at the start of year two, and then on to diff eq. When should I take linear algebra in that case? My adviser seemed...- sdefresco
- Thread
- Replies: 5
- Forum: STEM Academic Advising
-
I
[Linear Algebra] Maximal linear independent subset
Homework Statement In the follow cases find a maximal linearly independent subset of set ##A##: (a) ##A = \{(1,0,1,0),(1,1,1,1),(0,1,0,1),(2,0,-1,)\} \in \mathbb{R}^4## (b) ##A = \{x^2, x^2-x+1, 2x-2, 3\} \in \mathbb{k}[x]## The Attempt at a Solution The first part of the exercise is...- iJake
- Thread
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
I
[Linear Algebra] Linear transformation proof
Homework Statement Let ##V## and ##W## be vector spaces, ##T : V \rightarrow W## a linear transformation and ##B \subset Im(T)## a subspace. (a) Prove that ##A = T^{-1}(B)## is the only subspace of ##V## such that ##Ker(T) \subseteq A## and ##T(A) = B## (b) Let ##C \subseteq V## be a...- iJake
- Thread
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
I
Proving isomorphisms [Linear Algebra]
Homework Statement a) Let ##D_n(\mathbb{k}) = \{A \in M_n(\mathbb{k}) : a_{ij} = 0 \iff i \neq j\}## Prove that ## D_n(\mathbb{k}) \cong \mathbb{k}^n ## b) Prove that ##\mathbb{k}[X]_n \cong \mathbb{k}^{n+1}## I have one other exercise, but I would like to resolve it on my own. However, an...- iJake
- Thread
-
- Tags
- Algebra Linear algebra
- Replies: 10
- Forum: Calculus and Beyond Homework Help
-
V
Find monic generators of the ideals
Homework Statement Let ##T## be the linear operator on ##F^4## represented in the standard basis by $$\begin{bmatrix}c & 0 & 0 & 0 \\ 1 & c & 0 & 0 \\ 0 & 1 & c &0 \\ 0 & 0 & 1 & c \end{bmatrix}.$$ Let ##W## be the null space of ##T-cI##. a) Prove that ##W## is the subspace spanned by...- vbrasic
- Thread
-
- Tags
- Generators Linear algebra
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
I
[Linear Algebra] Help with Linear Transformations part 2
Homework Statement Homework Statement (a) Let ##V## be an ##\mathbb R##-vector space and ##j : V \rightarrow V## a linear transformation such that ##j \circ j = id_V##. Now, let ##S = \{v \in V : j(v) = v\}## and ##A = \{v \in V : j(v) = -v\}## Prove that ##S## and ##A## are subspaces and...- iJake
- Thread
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
I
[Linear Algebra] Help with Linear Transformation exercises
Homework Statement 1. (a) Prove that the following is a linear transformation: ##\text{T} : \mathbb k[X]_n \rightarrow \mathbb k[X]_{n+1}## ##\text{T}(a_0 + a_1X + \ldots + a_nX^n) = a_0X + \frac{a_1}{2}X^2 + \ldots + \frac{a_n}{n+1}## ##\text{Find}## ##\text{Ker}(T)## and ##\text{Im}(T)##...- iJake
- Thread
- Replies: 11
- Forum: Calculus and Beyond Homework Help
-
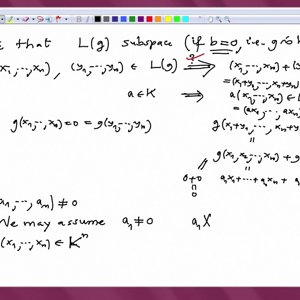
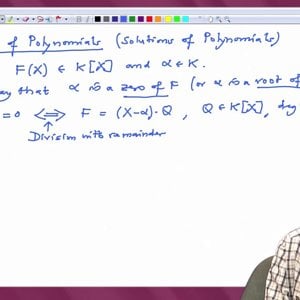
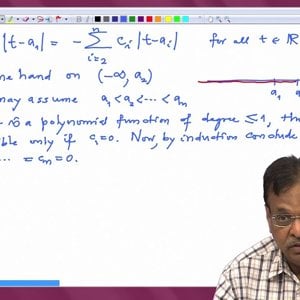
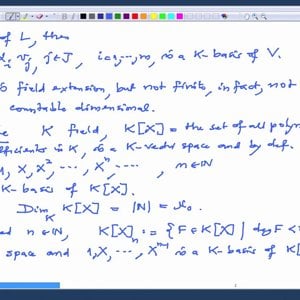
Linear Algebra by Prof. Dilip Patil (NPTEL):- Introductory video
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
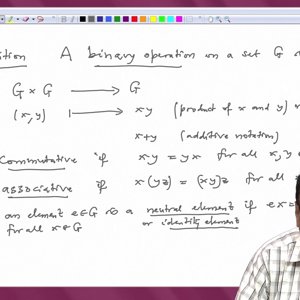
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 1: Introduction to Algebraic Structures - Rings and Fields
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
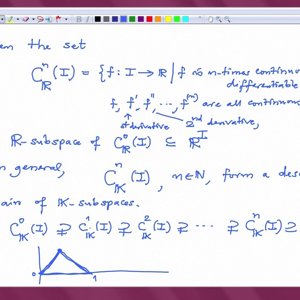
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 2: Defnition of Vector Spaces
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
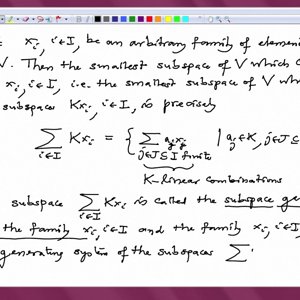
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 3: Examples of Vector Spaces
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 4: Defnition of subspaces
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 5: Examples of subspaces
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 6: Examples of subspaces continued
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 7: Sum of subspaces
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 8: System of linear equations
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 9: Gauss elimination
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 10: Generating system , linear independence and bases
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 11: Examples of a basis of a vector space
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 12: Review of univariate polynomials
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 13: Examples of univariate polynomials and rational functions
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 14: More examples of a basis of vector spaces
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 15: Vector spaces with finite generating system
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 16: Steinitzs exchange theorem and examples
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 17: Examples of finite dimensional vector spaces
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
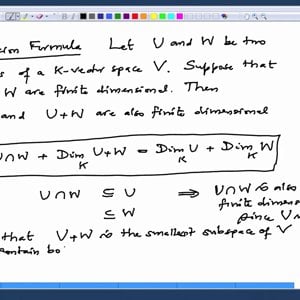
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 18: Dimension formula and its examples
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 19: Existence of a basis
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 20: Existence of a basis continued
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 21: Existence of a basis continued
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
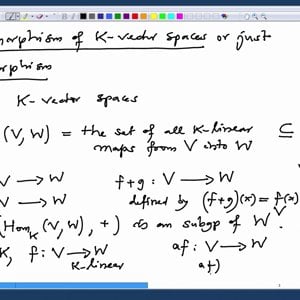
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 22: Introduction to Linear Maps
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 23: Examples of Linear Maps
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 24: Linear Maps and Bases
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 25: Pigeonhole principle in Linear Algebra
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 26: Interpolation and the rank theorem
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 27: Examples
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 28: Direct sums of vector spaces
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 29: Projections
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 30: Direct sum decomposition of a vector space
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 31: Dimension equality and examples
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 32: Dual spaces
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 33: Dual spaces continued
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 34: Quotient spaces
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 35: Homomorphism theorem of vector spaces
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra
-
Linear Algebra by Prof. Dilip Patil (NPTEL):- Lecture 36: Isomorphism theorem of vector spaces
COPYRIGHT strictly reserved to Prof. Dilip P. Patil and NPTEL, Govt. of India. Duplication prohibited. Lectures: http://www.nptel.ac.in/courses/111108098/ Syllabus: http://www.nptel.ac.in/syllabus/syllabus.php?subjectId=111108098- Wrichik Basu
- Media item
- linear algebra
- Comments: 0
- Category: Linear Algebra