Qft Definition and 980 Threads

In particle physics, the history of quantum field theory starts with its creation by Paul Dirac, when he attempted to quantize the electromagnetic field in the late 1920s. Major advances in the theory were made in the 1940s and 1950s, and led to the introduction of renormalized quantum electrodynamics (QED). QED was so successful and accurately predictive that efforts were made to apply the same basic concepts for the other forces of nature. By the late 1970s, these efforts successfully utilized gauge theory in the strong nuclear force and weak nuclear force, producing the modern standard model of particle physics.
Efforts to describe gravity using the same techniques have, to date, failed. The study of quantum field theory is still flourishing, as are applications of its methods to many physical problems. It remains one of the most vital areas of theoretical physics today, providing a common language to several different branches of physics.

View More On Wikipedia.org
Recent contents Top users
  1. bhobba

    A Interesting Paper On QFT and Quantum Measuremets

    I recently came across the following paper on QFT and Quantum Measurements. https://arxiv.org/abs/1311.0205 I have read it, but it may not be legit as it seems to accept the idea of virtual particles, which I find somewhat problematic, as discussed before. Before reaching any conclusions, I...
  2. Haorong Wu

    A Method of calculating the vacuum energy divergence

    In the book, quantum fields in curved space, when calculating the vacuum energy divergence for scalar fields, it reads: I could get the answer by letting ##k=m\tan t ## and using the properties of Beta functions and Gamma functions, but I still do not understand what it means by saying "with...
  3. M

    High Energy Possible typo in Peskin & Schroeder's QFT Textbook (p. 666)?

    Hi everyone! I'm going through Peskin & Schroeder's Chapter 19 (Perturbation Theory Anomalies) and it seems to be that equation 19.74 in page 666 has a minus sign missing on the RHS. Namely, I think the correct equation should read \begin{align} (i\not\!\! D)^2 = -D^2 -...
  4. norwegian_hobby_sci

    I Feedback on Educational Script: What's a particle in QFT?

    I'm trying to create a YouTube educational science video on Quantum Field Theory and the Standard Model. I'm not a physicist (just a hobby), and would love feedback on my explanation below, and help to point out (or rewrite) parts that are scientifically inacurate or misleading. Or just point me...
  5. MichPod

    I A probability of field amplitude in QFT

    Per quantized scalar field (quantized Klein-Gordon equation), suppose we act on a vacuum state |0> with some set of creation operators to have some particles. How then can we calculate a probability density for the field to have a particular value ##\psi_0## (upon measurement) at a specific...
  6. joneall

    A Don't understand equation with overleftrightarrow symbol

    I've started reading Srednicki's book on QFT, which was starting well. Then I hit on an equation which I just don't understand at all. Since I don't know what the symbol is called, I can only refer to it by its latex name. Here's the bit. Srednicki defines the following object: $$f...
  7. T

    A How can I calculate the square of the Pauli-Lubanski pseudovector?

    Hello there, recently I've been trying to demonstrate that, $$\textbf{W}^2 = -m^2\textbf{S}^2$$ in a rest frame, with ##W_{\mu}## defined as $$W_{\mu} = \dfrac{1}{2}\varepsilon_{\mu\alpha\beta\gamma}M^{\alpha\beta}p^{\gamma}$$ such that ##M^{\mu\nu}## is an operator of the form $$...
  8. S

    A Creation and annihilation operator

    Hey, I have a short question. The quantized field in Schrödinger picture is given by: \hat{\phi} \left(\textbf{x}\right) =\int \frac{d^{3}p}{\left(2\pi\right)^3} \frac{1}{\sqrt{\omega_{2\textbf{p}}}}\left(\hat{a}_{\textbf{p}}e^{i\textbf{p} \cdot \textbf{x}} +...
  9. Alpha2021

    Cross section for the decay of gauge bosons from a scalar field

  10. J

    A QFT S-matrix explanations are incomprehensible

    The first look at a scattering process is something like this: We define an initial state |\textrm{in}\rangle = \int dp_1dp_2 f_{\textrm{in,1}}(p_1) f_{\textrm{in,2}}(p_2) a_{p_1}^{\dagger} a_{p_2}^{\dagger} |0\rangle Here f_{\textrm{in,1}} and f_{\textrm{in,2}} are wavefunctions that define...
  11. haushofer

    A QFT for the gifted amateur: translation of prob. density

    Dear all, I was reading through the book "QFT for the gifted amateur" because I'm currently working on a popular science book about symmetries. Chapter 9 is about transformations of the wave function. On page 80 the book says It's the second equality that confuses me: doesn't the statement...
  12. DuckAmuck

    A Anti-symmetric tensor question

    The sigma tensor composed of the commutator of gamma matrices is said to be able to represent any anti-symmetric tensor. \sigma_{\mu\nu} = i/2 [\gamma_\mu,\gamma_\nu] However, it is not clear how one can arrive at something like the electromagnetic tensor. F_{\mu\nu} = a \bar{\psi}...
  13. E

    A The μ in dimensional regularization

    I have a question about the ##\mu## in dimensional regularization and how it is related to renormalization conditions. I follow the same notation and conventions as in Schwartz. Take QED as an example: $$\mathcal{L} =-\frac{1}{4}\left( F_{0}^{\mu \nu }\right)^{2} +\overline{\psi }_{0}\left(...
  14. G

    Deriving equations of motion of abelian gauge field coupled to scalar

    I want to compute the equations of motion for this theory in terms of the functions ##f## and ##a##. My plan was to apply the Euler-Lagrange equations, but it got confusing very quickly. Am I right that we'll have 3 sets of equations? One for each of the fields ##\phi,\phi^\dagger, A_\mu## ...
  15. G

    Computing path integral with real and Grassmann variables

    The first step seems easy: computation of the $\theta$ and $\overline{\theta}$ integrals give $$Z[w] = \frac{1}{(2\pi)^{n/2}}\int d^n x \: \det(\partial_j w_i(x)) \exp{\left(-\frac{1}{2}w_i(x)w_i(x)\right)}.$$ From here, I tried using that $$\det(\partial_j w_i (x)) = \det\left(\partial_j w_i...
  16. George Wu

    A What is a spatial wavefunction in QFT?

    My understanding is: $$\phi (\mathbf{k})=\int{d^3}\mathbf{x}\phi (\mathbf{x})e^{-i\mathbf{k}\cdot \mathbf{x}}$$ But what is ##\phi (\mathbf{x})## in Qft? In quantum mechanics, $$|\phi \rangle =\int{d^3}\mathbf{x}\phi (\mathbf{x})\left| \mathbf{x} \right> =\int{d^3}\mathbf{k}\phi...
  17. George Wu

    A Do Time-ordering and Time Integrals commute? Peskin(4.22)(4.31)(4.44)

    In Peskin P85: It says the Time-ordered exponential is just a notation，in my understanding, it means $$\begin{aligned} &T\left\{ \exp \left[ -i\int_{t_0}^t{d}t^{\prime}H_I\left( t^{\prime} \right) \right] \right\}\\ &\ne T\left\{ 1+(-i)\int_{t_0}^t{d}t_1H_I\left( t_1 \right)...
  18. S

    I Propagator of massless Weyl field

    I have this Lagrangian for a free massless left Weyl spinor, so it’s just the kinetic term, that can be written embedding the field into a larger Dirac spinor and then taking the left projector in this way: $$i \bar{\psi} \cancel{\partial} P_L \psi$$ Srednicki says that the momentum space...
  19. T

    I Why is there an additional prefactor in equation (12.52) of Peskin's QFT book?

    Hey all, I am currently having trouble understanding equation (12.52) in Peskin's QFT book. Specifically the term for external leg corrections, in which they tack on an additional prefactor of ##(-ig)##. Normally with external leg prefactors, we don't see the coupling constant multiplied onto...
  20. Sciencemaster

    I Finding ##\partial^\mu\phi## for a squeezed state in QFT

    I'm trying to apply an operator to a massless and minimally coupled squeezed state. I have defined my state as $$\phi=\sum_k\left(a_kf_k+a^\dagger_kf^*_k\right)$$, where the ak operators are ladder operators and fk is the mode function $$f_k=\frac{1}{\sqrt{2L^3\omega}}e^{ik_\mu x^\mu}$$...
  21. A

    I Exploring the Big Picture of QFT

    What is the big picture of QFT? I have studied quantum mechanics from: -Griffiths -the first few chapters of Sakurai -Ballentine I have studied electrodynamics from Griffiths and General Relativity from Carroll I have assigned level I to the question, but any answer is welcome
  22. D

    I QFT vs GR Cosmological Constant

    I am sorry but I can't seem to find the actual estimated value of the cosmological constant that is predicted by quantum field theory. Can anyone help me and tell me the approximation of that value and/or the value of the approximate observed cosmological constant that physicists today think...
  23. M

    Non quadratic potentials and quantization in QFT (home exercise)

    I noticed that ##V(\phi)## has nonzero minima, therefore I found the stationary points as ##{{\partial{V}}\over{\partial\phi}}=0##, and found the solutions: $$\phi^0_{1,2}=-{{m}\over{\sqrt{\lambda}}}\quad \phi^0_3={{2m}\over{\sqrt{\lambda}}}$$ of these, only ##\phi^0_3## is a stable minimum...
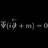
  24. qft-El

    A Heisenberg picture and Path integrals (Zee QFT)

    Reading the introduction to path integrals given in the latest edition of Zee's "Quantum field theory in a nutshell", I have found a remark which I don't really understand. The author is evaluating the free particle propagator ##K(q_f, t; q_i, 0)## $$\langle q_f\lvert e^{-iHt}\lvert q_i...
  25. V

    I Uncertainty Principle in QFT & Early Universe Conditions

    I have a question related to the uncertainty principle in QFT and if it is related to the early universe conditions. Do we still have four-vector momentum and position uncertainty relation in relativistic quantum theory? I have been following the argument related to the early universe and the...
  26. BiGyElLoWhAt

    A Question about factoring the Klein-Gordon equation

    Take the Klein-Gordon equation: ##\Box^2 = m^2## Say we want to linearize this equation, we try to come up with a new operator that squares into ##\Box^2##. ##(A\partial_t - B\partial_x - C\partial_y - D\partial_z)^2 = \Box^2## So we need ##-A^2=B^2=C^2=D^2=I## as this gives back the 2nd...
  27. W

    Quantum Suggestions for math/ math courses to take before QFT

    Hello, I was wondering what math/ math courses I should study or take before QFT. I've taken courses in linear algebra (one course), diff. equations, partial diff. equations. Thanks!
  28. BiGyElLoWhAt

    A How can you tell the spin of a particle by looking at the Lagrangian?

    I'm just starting to get into QFT as some self study. I've watched some lectures and videos, read some notes, and am trying to piece some things together. Take ##U(1)_{EM}: L = \bar{\psi}[i\gamma^{\mu}(\partial_{\mu} - ieA_{\mu}) - m]\psi - 1/4 F_{\mu\nu}F^{\mu\nu}## This allegedly governs spin...
  29. Marioweee

    QFT: Normalization of coherent states

    What I have done is the following: \begin{equation} \braket{\eta_k | \eta_k}=|N|^2\sum_{n=0}^{\infty}\dfrac{1}{n!}\bra{0}(A^{\dagger})^nA^n\ket{0}=|N|^2\sum_{n=0}^{\infty}\dfrac{1}{n!}\int...
  30. G

    I Why does the QFT Lagrangian not already use operators?

    I've learned that in canonical quantization you take a Lagrangian, transform to a Hamiltonian and then "put the hat on" the fields (make them an operator). Then you can derive the equations of motion of the Hamiltonian. What is the reason that you cannot already put hats in the QFT Lagrangian...
  31. C

    Quantum Discover the Best Lightweight QFT Introductions for Self-Study

    I was a denizen of this forum some 15 years ago during undergrad. However I since joined the dark side working in software on ML, AI, and distributed data processing. Every now and then I pick up a physics textbook to get into the weeds of a topic I would have missed due to skipping out on grad...
  32. snoopies622

    What are the basic mathematical objects in QFT?

    I found a copy of David McMahon's "Quantum Field Theory Demystified" and I'm already confused on page 4 where he says, " . . in order to be truly compatible with special relativity, we need to discard the notion that \phi and \psi in the Klein-Gordon and Dirac equations respectively describe...
  33. S

    Spin-1 particle states as seen by different observers: Wigner rotation

    Summary: Suppose that observer ##\mathcal{O}## sees a ##W## boson (spin-1 and ##m > 0##) with momentum ##\boldsymbol{p}## in the ##y##-direction and spin ##z##-component ##\sigma##. A second observer ##\mathcal{O'}## moves relative to the first with velocity ##\boldsymbol{v}## in the...
  34. apostolosdt

    Is Feynman the "wise guy" in Zee's QFT book?

    Zee, in his QFT in a nutshell, tells that beautiful story about a "wise guy" who, through his annoying questions to the professor, actually describes a fundamental principle of quantum mechanics, essential to Feynman's approach to quantum phenomena (pp. 9 in Zee's). Now, Zee appears to imply...
  35. G

    Tong QFT sheet 2, question 6: Normal ordering of the angular momentum operator

    My attempt/questions: I use ##T^{0i} = \dot{\phi}\partial^i \phi##, ##\dot{\phi} = \pi##, and antisymmetry of ##Q_i## to get: ##Q_i = 2\epsilon_{ijk}\int d^3x [x^j \partial^k \phi(\vec{x})] \pi(\vec{x})##. I then plug in the expansions for ##\phi(\vec{x})## and ##\pi(\vec{x})## and multiply...
  36. apostolosdt

    High Energy Another typo in Peskin & Schroeder's QFT?

    I'm using a Peskin & Schroeder's copy that looks like it has all typos corrected and I wonder if the following is an undetected typo: On pp. 103 and on the RHS of the bra expression just after (4.68), shouldn't the ##\phi_f({\mathbf p}_f)## be complex conjugated?
  37. dextercioby

    A First order electroweak correction to the g-2 magnetic moment

    We know that we need to go to 5th order in perturbation theory to match 10 decimals of g-2 for electron, theory vs. experiment. But let us not assume QED is pure and independent, but it's a lower energy limit of GSW (not Green-Schwartz-Witten from superstrings) electroweak theory. Has anyone...
  38. A

    I Can entanglement occur in distant galaxies according to NRQM and QFT?

    What is entanglement in QM and QFT? I understood that it only corresponds to the concept of linear combination of states with multiple particles. Seeing lectures on YB it seems to me that it is something much deeper than that. What did I miss? How is it treated in QFT? I am studying NRQM from...
  39. A

    I Acceleration in QFT: Fundamentals, Causes, Quantization

    What is acceleration in QFT at the fundamental level? What causes it? Is it quantized? Is there a connection between acceleration in QFT and the equivalence principle?
  40. gremory

    A S-Matrix in Quantum Field Theory

    Hello, i need help with the S-matrix. From what i understand, with the S-matrix i would be able to compute the scattering amplitude of some processes, is that correct? If so, how would i be able to do that if i have some field ##\phi(x,t)## in hands? Is that possible?
  41. gremory

    A Computing Correlation functions

    Hello, recently I'm learning about correlation functions in the context of QFT. Correct me with I'm wrong but what i understand is that tha n-point correlation functions kinda of describe particles that are transitioning from a point in space-time to another by excitations on the field. So, what...
  42. Tommy White

    B Exploring QFT: Is It Understandable?

    I'm not even sure whether it can be defined in QFT, but I got this from SE: Which I don't understand. I'm not mathematically sophisticated enough for that.
  43. A

    What are some recommended textbooks for learning QFT?

    Which textbook is recommended for a modern introduction to QFT? What mathematical topics do I need to know to start studying QFT? From which textbooks can I learn them? I know calculus, linear algebra, mathematical methods of physics (the necessary topics for quantum mechanics). I learned basic...
  44. J

    Lagrangian with a charged, massive vector boson coupled to electromagnetism

    I need to use hermiticity and electromagnetic gauge invariance to determine the constraints on the constants. Through hermiticity, i found that the coefficients need to be real. However, I am not sure how gauge invariance would come into the picture to give further contraints. I think the...
  45. E

    I Schwartz derivation of the Feynman rules for scalar fields

    Hi everyone, In his book "Quantum field theory and the standard model", Schwartz derives the position-space Feynman rules starting from the Schwinger-Dyson formula (section 7.1.1). I have two questions about his derivation. 1) As a first step, he rewrites the correlation function as $$...
  46. N

    A Noether and the derivative of the Action

    I know that the Action has units Energy·time or Momentum·position. A second fact is that the derivative of the action with respect to time is Energy and similar with momentum-position, consistent with a units ie. dimensions check.Is it a coincidence that both are Noether conserved quantities...
  47. J

    A Generalized Forces and QED/QCD

    In Lagrangian mechanics we learn about generalized forces. However, I haven't seen these explicitly mentioned in books on QFT. Can the Lagrangians of QED or QCD be expressed in terms of generalized forces or is there some connection there, in particular to the Nielsen form.
  48. E

    I When to use Feynman or Schwinger Parametrization

    I had been doing some calculations involving propagators with both a quadratic and a linear power of loop momentum in the denominator. In the context of HQET and QCD with strategy of regions. The texts which I am following sometimes tend to straightaway use Schwinger and I am just wondering if...
  49. M

    A QED Formulation with Massive Photon Fields

    I was reading Diagrammatica by Veltman and he treats the photon field as a massive vector boson in which gauge invariance is disappeared and the propagator has a different expression than in massless photon. After some googling, I found that this is one way to formulate QED which has the...
  50. Question69

    B Unitarity in GR+QFT: Obeying Full QG Model?

    Does unitarity have to be obeyed in a full quantum gravity model?
Back
Top