What is Representation theory: Definition and 67 Discussions

Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studies modules over these abstract algebraic structures. In essence, a representation makes an abstract algebraic object more concrete by describing its elements by matrices and their algebraic operations (for example, matrix addition, matrix multiplication). The theory of matrices and linear operators is well-understood, so representations of more abstract objects in terms of familiar linear algebra objects helps glean properties and sometimes simplify calculations on more abstract theories.The algebraic objects amenable to such a description include groups, associative algebras and Lie algebras. The most prominent of these (and historically the first) is the representation theory of groups, in which elements of a group are represented by invertible matrices in such a way that the group operation is matrix multiplication.Representation theory is a useful method because it reduces problems in abstract algebra to problems in linear algebra, a subject that is well understood. Furthermore, the vector space on which a group (for example) is represented can be infinite-dimensional, and by allowing it to be, for instance, a Hilbert space, methods of analysis can be applied to the theory of groups. Representation theory is also important in physics because, for example, it describes how the symmetry group of a physical system affects the solutions of equations describing that system.Representation theory is pervasive across fields of mathematics for two reasons. First, the applications of representation theory are diverse: in addition to its impact on algebra, representation theory:

illuminates and generalizes Fourier analysis via harmonic analysis,
is connected to geometry via invariant theory and the Erlangen program,
has an impact in number theory via automorphic forms and the Langlands program.Second, there are diverse approaches to representation theory. The same objects can be studied using methods from algebraic geometry, module theory, analytic number theory, differential geometry, operator theory, algebraic combinatorics and topology.The success of representation theory has led to numerous generalizations. One of the most general is in category theory. The algebraic objects to which representation theory applies can be viewed as particular kinds of categories, and the representations as functors from the object category to the category of vector spaces. This description points to two obvious generalizations: first, the algebraic objects can be replaced by more general categories; second, the target category of vector spaces can be replaced by other well-understood categories.

View More On Wikipedia.org
Recent contents Top users
  1. LCSphysicist

    I Page 183-184 of Howard George's group book

    I would appreciate if someone could help me to understand what is happening in section 12.3 from the Howard George's book. First of all, the propose of the section is to show how $SU(3)$ decomposes into $SU(2) \times U(1)$. But i can't understand what is happening. First of all, i can't get the...
  2. T

    A Classification of reductive groups via root datum

    I have a couple of questions about classification of reductive groups over algebraically closed field (up to isomorphism) by so called root datum. In the linked discussion is continued that Obviously, a root datum ##(X^*, \Phi, X_*, \phi^{\vee})## contains full information ("building plan")...
  3. A

    Regarding commutative Lie groups and irreducible rep

    Above
  4. A

    About representations of Lie groups

    I am not quite sure of how this works, i.e. of what exactly I need to do with the hint. Any explanantion would be helpful!
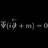
  5. qft-El

    A In what representation do Dirac adjoint spinors lie?

    I hope this is the right section as the question is about Lie groups and representations. First and foremost, in this post I'll be dealing with Dirac and Weyl spinor (not spinor fields) representations of the Lorentz algebra. Also, for simplicity, I'll use the chiral representation later on...
  6. K

    I Tensor decomposition, Sym representations and irreps.

    New to group theory. I have 3 questions: 1. Tensor decomposition into Tab = T[ab] +T(traceless){ab} + Tr(T{ab}) leads to invariant subspaces. Is this enough to imply these subreps are irreducible? 2. The Symn representations of a group are irreps. Why? 3. What is the connection between...
  7. H

    A Von Neumann's uniqueness theorem (CCR representations)

    Hi Pfs, Please read this paper (equation 4): https://ncatlab.org/nla b/files/RedeiCCRRepUniqueness.pdf It is written: Surprise! P is a projector (has to be proved)... where can we read the proof?
  8. P

    A Questions about representation theory of Lie algebra

    I have confusions about representation theory. In the following questions, I will try to express it as best as possible. For this thread say representation is given as ρ: L → GL(V) where L is the Lie group(or symmetry group for a physicist) GL(V) is the general linear...
  9. L

    A Unitary representations of Lie group from Lie algebra

    In Quantum Mechanics, by Wigner's theorem, a symmetry can be represented either by a unitary linear or antiunitary antilinear operator on the Hilbert space of states ##\cal H##. If ##G## is then a Lie group of symmetries, for each ##T\in G## we have some ##U(T)## acting on the Hilbert space and...
  10. L

    Finding Cartan Subalgebras for Matrix Algebras

    This is one problem from Robin Ticciati's Quantum Field Theory for Mathematicians essentially asking us to find Cartan subalgebras for the matrix algebras ##\mathfrak{u}(n), \mathfrak{su}(n),\mathfrak{so}(n)## and ##\mathfrak{so}(1,3)##. The only thing he gives is the definition of a Cartan...
  11. filip97

    A Why Spinors Are Irreducible if Gamma-Traceless: Explained

    I read this question https://physics.stackexchange.com/questions/95970/under-what-conditions-is-a-vector-spinor-gamma-trace-free . Also I read Sexl and Urbantke book about groups. But I don't understand why spinors is irreducible if these are gamma-tracelees. Also I read many papers about...
  12. filip97

    A (A,A) representation of Lorentz group-why is it tensor?

    Why representation of Lorentz group of shape (A,A) corespond to totally symmetric traceless tensor of rank 2A? For example (5,5)=9+7+5+3+1 (where + is dirrect sum), but 1+5+3+9+7<>(5,5) implies that (5,5) isn't symmetric ? See Weinberg QFT Book Vol.1 page 231.
  13. N

    A Block Diagonalization - Representation Theory

    How does one go about finding a matrix, U, such that U-1D(g)U produces a block diagonal matrix for all g in G? For example, I am trying to figure out how the matrix (7) on page 4 of this document is obtained.
  14. Ramtin123

    A Why Is the Mixed SU(2) Term Invariant in Scalar Multiplet Models?

    Consider two arbitrary scalar multiplets ##\Phi## and ##\Psi## invariant under ##SU(2)\times U(1)##. When writing the potential for this model, in addition to the usual terms like ##\Phi^\dagger \Phi + (\Phi^\dagger \Phi)^2##, I often see in the literature, less usual terms like: $$\Phi^\dagger...
  15. tomdodd4598

    I Exploring Direct Sums of Lorentz Group Representations

    Hey there, I've suddenly found myself trying to learn about the Lorentz group and its representations, or really the representations of its double-cover. I have now got to the stage where the 'complexified' Lie algebra is being explored, linear combinations of the generators of the rotations...
  16. Hans de Vries

    A New Covariant QED representation of the E.M. field

    90 years have gone by since P.A.M. Dirac published his equation in 1928. Some of its most basic consequences however are only discovered just now. (At least I have never encountered this before). We present the Covariant QED representation of the Electromagnetic field. 1 - Definition of the...
  17. A

    I Adjoint Representation Confusion

    I'm having a bit of an issue wrapping my head around the adjoint representation in group theory. I thought I understood the principle but I've got a practice problem which I can't even really begin to attempt. The question is this: My understanding of this question is that, given a...
  18. Cryo

    A Nonlinear susceptibility and group reps

    Dear All short explanation: I am trying to leverage my limited understanding of representation theory to explain (to myself) how many non-vanshing components of, for example, nonlinear optical susceptibility tensor ##\chi^{(2)}_{\alpha\beta\gamma}## can one have in a crystal with known point...
  19. Ramtin123

    A Three dimensional representation of ##U(1)\times SU(2)##

    Consider a three dimensional representation of ##U(1)\times SU(2)## with zero hypercharge ##Y=0##: $$ L= \begin{pmatrix} L^+ \\ L^0 \\ L^- \end{pmatrix} $$ Then the mass term is given by [1]: $$ \mathcal{L} \supset -\frac m 2 \left( 2 L^+ L^- +L^0 L^0 \right) $$ I am wondering where the...
  20. C

    I Lorentz Group: Tensor Representation Explained

    I've been trying to understand representations of the Lorentz group. So as far as I understand, when an object is in an (m,n) representation, then it has two indices (let's say the object is ##\phi^{ij}##), where one index ##i## transforms as ##\exp(i(\theta_k-i\beta_k)A_k)## and the other index...
  21. JuanC97

    I Minimum requisite to generalize Proca action

    Hello guys, In 90% of the papers I've read about diferent ways to achieve generalizations of the Proca action I've found there's a common condition that has to be satisfied, i.e: The number of degrees of freedom allowed to be propagated by the theory has to be three at most (two if the fields...
  22. JuanC97

    I ##A_\mu^a=0## in global gauge symmetries ?

    Hi, this question is related to global and local SU(n) gauge theories. First of all, some notation: ##A## will be the gauge field of the theory (i.e: the 'vector potential' in the case of electromagnetic interactions) also known as 'connection form'. In components: ##A_\mu## can be expanded in...
  23. Luck0

    A Diagonalizing Hermitian matrices with adjoint representation

    Suppose I have a hermitian ##N \times N## matrix ##M##. Let ##U \in SU(N)## be the matrix that diagonalizes ##M##: ##M = U\Lambda U^\dagger##, where ##\Lambda## is the matrix of eigenvalues of ##M##. This transformation can be considered as the adjoint action ##Ad## of ##SU(N)## over its...
  24. S

    I Representation Theory clarification

    Hello! I am reading some things about representation theory for SU(n) and I want to make sure I understand it properly. I will put an example here and explain what I understand out of it and I would really appreciate if someone can tell me if it is right or not. So for SU(2) we have ##2 \otimes...
  25. L

    A Tensor symmetries and the symmetric groups

    In one General Relativity paper, the author states the following (we can assume tensor in question are tensors in a vector space ##V##, i.e., they are elements of some tensor power of ##V##) To discuss general properties of tensor symmetries, we shall use the representation theory of the...
  26. pellis

    A Who wrote "Ch 6 Groups & Representations in QM"?

    Who really wrote the best introductory account of representation theory in QM that I've seen so far ? [Likely mis-attribution discussed here below; prefixed "Advanced" to reach lecturers who are more likely to know the answer to this question.] It's available via...
  27. S

    I Normal modes using representation theory

    Hello! I am reading some representation theory (the book is Lie Algebra in Particle Physics, by Georgi, part 1.17) and the author solves a problem of 3 bodies connected by springs forming a triangle, aiming to find the normal modes. He builds a 6 dimensional vector formed of the 3 particles and...
  28. P

    Massive spin-s representations of the Poincare group

    Context The following is from the book "Ideas and methods in supersymmetry and supergravity" by I.L. Buchbinder and S.M Kuzenko, pg 56-60. It is about realizing the irreducible massive representations of the Poincare group as spin tensor fields which transform under certain representations of...
  29. M

    A Representation theory of supersymmetry

    I had heard of adinkras but didn't realize that they were meant to play this role. Nor did I realize that the representation theory of supersymmetry is mathematically underdeveloped.
  30. arivero

    I Bootstraping a space from its tensor square

    By space, I mean a vector space which could be a representation of a group or even have some expanded algebraic structure. So I am not sure if this question goes here or in the Algebra subforum. Consider the tensor square r\otimes r of an irreducible group representation r with itself, and...
  31. V

    A How parity exchanges right handed and left handed spinors

    Reading through David Tong lecture notes on QFT.On pages 94, he shows the action of parity on spinors. See below link: [1]: http://www.damtp.cam.ac.uk/user/tong/qft/qft.pdfIn (4.75) he confirms that parity exchanges right handed and left handed spinors. Or for an arbitrary representation of...
  32. B

    A Notation/Site for Representations of an Algebra

    I'm currently reading the paper "Higher Spin extension of cosmological spacetimes in 3d: asymptotically flat behaviour with chemical potentials in thermodynamics" I'm looking at equation (3) on page 4. I know that symmetrization brackets work like this A_(a b) = (A_ab + A_ba)/2. However I have...
  33. Twigg

    A Is representation theory worthwhile for quantum?

    Recently I read some comment on Sakurai's book (which I have not read) that the writer of said comment didn't understand part of the text until they understood irreducible representations. I do not know to what they were referring, but it piqued my interest in representation theory. My question...
  34. S

    I No problem, it's always good to have multiple sources!

    Hello. If I represent a vector space using matrices, for example if a 3x1 vector, V, is represented by 3x3 matrix, A, and if this vector was the eigenvector of another matrix, M, with eigenvalue v, if I apply M to the matrix representation of this vector, does this holds: MA=vA? Also, if I...
  35. S

    I Understanding SU(2) Representations and Their Role in Particle Physics

    Hello! I just started reading about SU(2) (the book is Lie Algebras in Particle Physics by Howard Georgi) and I am confused about something - I attached a screenshot of those parts. So, for what I understood by now, the SU(2) are 2x2 matrices whose generators are Pauli matrices and they act on a...
  36. G

    I About Lie group product ([itex]U(1)\times U(1)[/itex] ex.)

    I recently got confused about Lie group products. Say, I have a group U(1)\times U(1)'. Is this group reducible into two U(1)'s, i.e. possible to resepent with a matrix \rho(U(1)\times U(1)')=\rho_{1}(U(1))\oplus\rho_{1}(U(1)')=e^{i\theta_{1}}\oplus e^{i\theta_{2}}=\begin{pmatrix}e^{i\theta_{1}}...
  37. I

    Courses Representation theory or algebraic topology

    Hello everyone, I'm a undergraduate at UC Berkeley. I'm doing theoretical physics but technically I'm a math major. I really want to study quantum gravity in the future. Now I have a problem of choosing courses. For next semester, I have only one spot available for either representation theory...
  38. Giuseppe Lacagnina

    Lorentz transformations and vector fields

    Hi Everyone. There is an equation which I have known for a long time but quite never used really. Now I have doubts I really understand it. Consider the unitary operator implementing a Lorentz transformation. Many books show the following equation for vector fields: U(\Lambda)^{-1}A^\mu...
  39. JonnyMaddox

    Explicitly Deriving Spinor Representations from Lorentz Group

    I'm currently reading a book on relativistic field theory and I'm trying to understand spinors. After the author introduces the four parts of the Lorentz group he talks about spinors and group representations: "...With this concept we see that the 2x2 unimodular matrices A discussed in the...
  40. B

    Algebra Good book on representation theory of groups

    Hi I am a physics graduate student. Recently I am learning representation theory of groups. I understand the basic concepts. But I need a good book with lots of examples in it and also exercise problems on representation theory so that I can brush up my knowledge.The text we follow is "Lie...
  41. Dilatino

    Introduction to Young-tableaux and weight diagrams?

    I am looking for a short pedagogical introduction to Young-tableaux and weight diagrams and the relationship between them, which contains many detailled and worked out examples of how these methods are applied in physics, such as in the context of the standard model and beyond for example. I am...
  42. terra

    2j+1 d representation for Poincaré group

    I want to learn how to write down a particle state in some inertial coordinate frame starting from the state ##| j m \rangle ##, in which the particle is in a rest frame. I know how to rotate this state in the rest frame, but how does one write down a Lorentz boost for it? Note that I am not...
  43. Primroses

    Why are invariant tensors also Clebsch-Gordan coefficients?

    On one hand, in reading Georgi's book in group theory, I comprehend the invariant tensor as a special "tensor", which is unchanged under the action of any generators. On the other hand, CG decomposition is to decompose the product of two irreps into different irreps. Now it is claimed that...
  44. T

    Young tableux (representation theory)

    Homework Statement Consider the irreducible representation V in the symmetric group S_5 corresponding to the Young diagram (these are meant to be boxes): [\;\;][\;\;] \\ [\;\;][\;\;] \\ [\;\;]\;\;\;\; (a) List all standard Young tableaux of the given shape (that is, list all the possible...
  45. T

    Representation Theory: Proving Invariant Subspaces and Decomposition Properties

    Homework Statement I think I've done (a) and (b) correctly (please check). I'm stuck as to how to describe all subspaces of V that are preserved by the operators \varphi(t) and how to prove that \varphi can't be decomposed into a direct sum \varphi = \varphi |_U \oplus \varphi |_{U'}...
  46. V

    Representation theory question

    I'm self-studying representation theory for finite groups using "Group Theory and Quantum Mechanics" by Michael Tinkham. Most of it makes sense to me, but I'm having difficulty understanding what is meant by saying a function "belongs to a particular irreducible representation", or "has the...
  47. pellis

    Dumb question about representation theory?

    It seems that there’s a loose way of discussing group representations that’s fine for the initiated, but confusing for the neophyte: I understand that the objects that represent group operations are usually (or always?) square matrices, which naturally can be described as “matrix...
  48. P

    Help solving a problem on representation theory

    Homework Statement Hi all, I'm having to solve a few exercises from the book "Introduction to representation theory" (Etingof, Goldberg,...), and I am stuck on an exercise. In the book it's number 5.16.2: The content c(\lambda) of a Young diagram \lambda is the sum...
  49. Math Amateur

    Representation Theory of Finite Groups - CH 18 Dummit and Foote

    I am reading Dummit and Foote on Representation Theory CH 18 I am struggling with the following text on page 843 - see attachment and need some help. The text I am referring to reads as follows - see attachment page 843 for details \phi ( g ) ( \alpha v + \beta w ) = g \cdot ( \alpha v +...
  50. M

    Representation theory and totally symmetric ground state?

    Hello My question is about the ground state of vibrations for a solid. I'm working with graphite and have found out that for k=0 (The Gamma symmetry point), the vibrational modes can be decomposed into irreducible represenations in the following way Vibration = 2 * E1u + 2 * E2g + 2 * A2u...
Back
Top