Archived How Does Bernoulli's Equation Determine Flow and Pressure in a Tank System?

[momogiri]

Water flows steadily from an open tank as in the figure below. The elevation of point 1 is 10.0m, and the elevation of points 2 and 3 is 2.00m. The cross-sectional area at point 2 is 0.0480m^2; at point 3 it is 0.0160m^2. The area of the tank is very large compared with the cross-sectional area of the pipe.

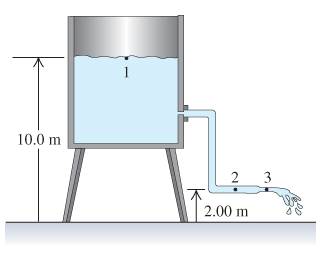
Part A is "Assuming that Bernoulli's equation applies, compute the discharge rate in cubic meters per second."
Which I've solved using Bernoulli's principle

so Q_3 = 0.200m^3/s

Part B is "What is the gauge pressure at point 2?"
Now this one I'm stuck with, but here's what I've done:

A_2*v_2 = A_3*v_3
(0.048)v_2 = (0.2)(0.016)

v_2 = 0.0666667m/s

so using Bernoulli's principle..(and cancelling some stuff)

P_2 + 0.5*rho*v_2^2 = P_3 + 0.5*rho*v_3^2
which becomes
P_2 + (0.5)(1000)(0.0666667)^2 = 101300 + (0.5)(1000)(0.2)^2
thus P_2 = 101317.7778

And I figured since gauge pressure meant P_G = P - atm
I subtracted 101317.7778 by 101300
which got me 17.7778 as my gauge pressure...
So what am I doing wrong? I don't seem to be getting the right answer here...

 

[MexChemE]

For part A, we apply Bernoulli and the continuity equation from point 1 to point 3
A_1 v_1 = A_3 v_3
P_1 + \frac{1}{2} \rho v_1^2 + \rho g h_1 = P_3 + \frac{1}{2} \rho v_3^2 + \rho g h_3
Since the tank is open, P_1 = P_3, so we have
v_3^2 - v_1^2 = 2g (h_1-h_3)
v_3^2 \left(1 - \left( \frac{A_3}{A_1} \right)^2 \right) = 2g (h_1-h_3)
Now, since the area of the tank is very large compared to the area of the jet, 1 - \left( \frac{A_3}{A_1} \right)^2 \approx 1, then
v_3 = \sqrt{2g (h_1-h_3)} = \sqrt{2 \left( 9.8 \ \frac{m}{s^2} \right) (10 \ m - 2 \ m)} = 12.52 \ \frac{m}{s}
So the flow rate is
Q = (0.016 \ m^2) \left(12.52 \ \frac{m}{s} \right) = 0.2 \ \frac{m^3}{s}

For part B, we apply Bernoulli and the continuity equation from point 2 to point 3
A_2 v_2 = A_3 v_3
P_2 + \frac{1}{2} \rho v_2^2 + \rho g h_2 = P_3 + \frac{1}{2} \rho v_3^2 + \rho g h_3
Points 2 and 3 have the same elevation, so we have
P_2 + \frac{1}{2} \rho v_2^2 = P_3 + \frac{1}{2} \rho v_3^2
We can calculate v_2 with the continuity equation
v_2 = \left( \frac{0.016 \ m^2}{0.048 \ m^2} \right) \left( 12.52 \ \frac{m}{s} \right) = 4.17 \ \frac{m}{s}
Now we calculate the pressure at point 2
P_2 = P_3 + \frac{1}{2} \rho (v_3^2 - v_2^2) = 101325 \ Pa + \frac{1}{2} \left(1000 \ \frac{kg}{m^3} \right) \left( \left(12.52 \ \frac{m}{s} \right)^2 - \left(4.17 \ \frac{m}{s} \right)^2 \right) = 171006 \ Pa
Finally, we calculate the gauge pressure
p_2 = P_2 - p_{atm} = 171006 \ Pa - 101325 \ Pa = 70 \ kPa

 

[victor oluvic]

what if there was a part of the question that says
(b)How much liquid will escape in 1 minute?

 

[MexChemE]

what if there was a part of the question that says
(b)How much liquid will escape in 1 minute?

The correct way of doing it would be to take into account the variation of the liquid level inside the tank with respect to time.

Do you know how to set up the mass balance for the tank in terms of a differential equation?