karush
Gold Member
MHB
- 3,240
- 5
View attachment 9364
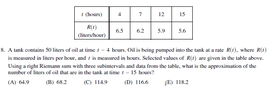
ok basically t is 3 hours appart except between 7 and 12 of which I didn't know if we should intemperate.
other wise it is just adding up the 4 $(t)\cdot(R(t))$s.
ok basically t is 3 hours appart except between 7 and 12 of which I didn't know if we should intemperate.
other wise it is just adding up the 4 $(t)\cdot(R(t))$s.
Attachments
Last edited: