wbetting
- 24
- 0
Homework Statement
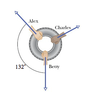
in a two-dimensional tug-of-war, Alex, Betty, and Charles pull horizontally on an automobile tire at the angles shown in the picture. The tire remains stationary in spite of the three pulls. Alex pulls with force of magnitude 211 N, and Charles pulls with force of magnitude 181 N. Note that the direction of is not given. What is the magnitude of Betty's force if Charles pulls in (a) the direction drawn in the picture or (b) the other possible direction for equilibrium?
** I got part a correct but i just do not understand what part b is looking
Homework Equations
for part a i used Fb= -fa-Fc
found angle of fa = 180-42= 138
fby=-fay-fcy
fbsin(-90)=-fasin138-fcsintheta
then did same thing with x components to get angle theta= 29.97 then plugged that angle into formula -fb=-(211N0(sin138)-181N(sin 29.97)
= 321.60 N
I understand that but how do i do the other possible direction? The question does not even make sense to me