ja!mee
- 16
- 0
Homework Statement
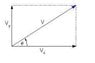
Okay so here is the problem: A golf ball is struck and leaves the ground at 96 m/s on a 60 angle. Determine the velocity of the ball 2 seconds after it was struck. I have the answer provided, which is 32.6 m/s at 45° above the horizon.
Homework Equations
Obviously I need to use the kinematic equations to solve this, and I have a hunch that I will need the Pythagoras as well.
The Attempt at a Solution
So what I have done is split the initial velocity of 96 m/s into a horizontal component and a vertical component. the horizontal being 48 m/s and the vertical 83.14. and now I am at a loss on how to proceed next... Not sure if I am over thinking the solution, but please help