Meco
- 8
- 0
Homework Statement
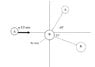
The drawing shows a collision between two balls. Ball A has a mass of .030kg and is moving along the x-axis with a velocity of +5.5 m/s. It makes a collision with ball B, which has a mass of .055kg and is initially at rest. The collision is not head-on. After the collision, the two balls fly apart with the angles shown in the drawing below
What is the final velocity of ball A and B?
... ... | Ball A
... ... | 65°
. A ---B---
... ... | 37°
... ... | Ball B
Can't get above picture to look right, going to take a picture of it and save it in the post
A and B show the start position and Ball A and Ball B shows where they finish
Homework Equations
M1V1 + M2V2 = M1V1'+ M2V2'
Using inverse trig?
The Attempt at a Solution
I saw basically the same problem in Khan's academy and in there he had one of the two ball's final velocity given. I have no real idea how to solve for two variables but here was my try:
Momentum in X initial= 5.5 * .03 = .165
Momentum in Y initial= 0
m1v1+ m2v2= m1v1'+ m2v2'
.030*5.5 + 0 = .03v1' +.055v2'
Attachments
Last edited: