3(x^2 + y^2)^2 = 25(x^2 - y^2) implicit differentiation

[LearninDaMath]

Use implicit differentiation to find the slope of the tangent line to the curve at the specified point.

3(x^2 + y^2)^2 = 25(x^2 - y^2) ; (2,1)

This is where I'm stuck:

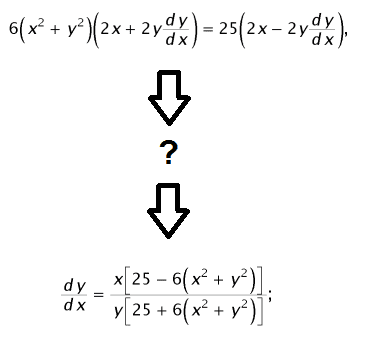
I know how to get up to the first equation...and I know how to get to the final answer from the second equation, but I have no clue how to get from the first equation in the picture to the second in the picture.It kind of reminds me of this:

Please help me if you could...I tried factoring out the twos, I just can't figure out how to get the same polynomial in the numerator and denominator...i mean, how the heck do the twos disappear? How does the 25 appear in both the numerator and denominator? I don't understand what steps are being taken here.

 

[HallsofIvy]

If you had A+ Bx= C+ Dx, how would you solve for x?

 

[I like Serena]

Hmm.
Let's make it a little more explicit (if you don't mind HoI).

You have:
$$6(x^2+y^2)(2x+2y{dy \over dx}) = 25(2x-2y{dy \over dx})$$

Let's define:
$$\begin{array}{l}A=6(x^2+y^2)\\B=2x\\C=2y\\z={dy \over dx}\end{array}$$
Then your equation becomes:
$$A(B+Cz)=25(B-Cz)$$
Do you know how to solve such an equation for z?

 

[LearninDaMath]

Hmm.
Let's make it a little more explicit (if you don't mind HoI).

You have:
$$6(x^2+y^2)(2x+2y{dy \over dx}) = 25(2x-2y{dy \over dx})$$

Let's define:
$$\begin{array}{l}A=6(x^2+y^2)\\B=2x\\C=2y\\z={dy \over dx}\end{array}$$
Then your equation becomes:
$$A(B+Cz)=25(B-Cz)$$
Do you know how to solve such an equation for z?

Well, i gave it a try and got \frac{B(A-25)}{-C(A+25)} = z

I multiplied A into (B+Cz) to get (AB+ACz). Then multiplied 25 into (B - Cz) to get (25B - 25Cz). Next, I got all the z terms on one side and everything else on the other. Then factored out the z from both terms and divided to isolate the z. Then I factored out B from the numerator and C from the denominator.

Is that correct?

 

[I like Serena]

Yes, that is correct.

Now replace A,B,C, and z by the definitions for them?

 

[LearninDaMath]

Got it, thanks much! Is the formula you presented one that fits a type of equation that comes up often? Are there like a group of general formulas such as the one you presented intended for various equations? I wonder if this is something that was covered in college algebra. My job schedule (military) pulled me out of class at the beginning of that semester for a couple weeks and so I told my professor i'd retake the course the following semester. When I went to sign up again, I found that the professor decided to pass me with a C. I was ecstatic at the time, but now it seems college algebra would make things a lot less confusing in calculus. I'm getting by, but it's taking a lot of extra studying. I really appreciate the help.

 

[I like Serena]

You're welcome. :)

It's a pretty standard method to give sub expressions names in the form of a single letters.
Then replace them by the letter, do whatever you need to, and replace the letters again by the sub expressions.

Edit: Oh, and I liked the picture with the blackboard you included. ;)

 

[LearninDaMath]

You're welcome. :)

It's a pretty standard method to give sub expressions names in the form of a single letters.
Then replace them by the letter, do whatever you need to, and replace the letters again by the sub expressions.

Edit: Oh, and I liked the picture with the blackboard you included. ;)

Thanks, feel free to use that picture whenever. I heard about it a while ago when watching some youtube video of a talk by an engineer turned biologist at a conference. Just search up "and then a miracle occurs" and you'll get a few variations of this picture.