- #1
DaveC426913
Gold Member
- 22,791
- 6,498
I am 99.5% sure I've got it right, but I keep second-guessing myself.
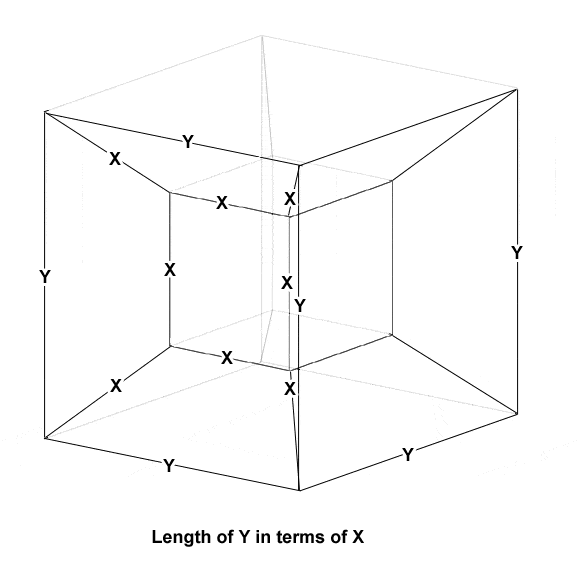
1] Cube with sides of length X.
2] Diagonals out from each corner of length no less than X...
3] ...to an outer cube of sides of length Y.
What must be the (shortest) length of Y in terms of X?
I get [tex] y = 2\sqrt{2}x[/tex]
1] Cube with sides of length X.
2] Diagonals out from each corner of length no less than X...
3] ...to an outer cube of sides of length Y.
What must be the (shortest) length of Y in terms of X?
I get [tex] y = 2\sqrt{2}x[/tex]
Attachments
Last edited:
