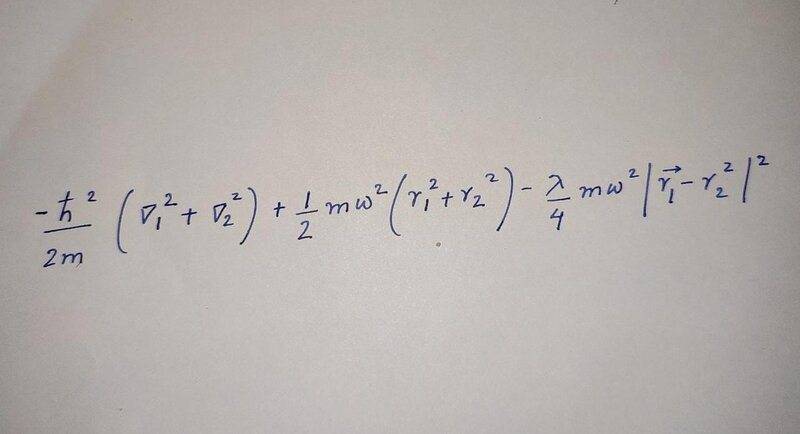Find Ground State Energy of 3D Harmonic Oscillator

koustav
Messages
29
Reaction score
4
Thread moved from the technical forums and poster has been reminded to show their work
Summary:: I am trying to find the exact ground state energy of the hamiltonian.kindly help me with this

WhatsApp Image 2021-05-12 at 4.36.13 PM.jpeg
 
Physics news on Phys.org
I suggest rewriting your equation in terms of new variables:

##\vec{R} = \frac{1}{2} (\vec{r}_1 + \vec{r}_2)##
##\vec{r} = \vec{r}_1 - \vec{r}_2##
 
Reply
  • Like
Likes Twigg and Haborix
To the OP, would you clarify the typo in the last term, just so we are all certain what we're working with.
 
Haborix said:
To the OP, would you clarify the typo in the last term, just so we are all certain what we're working with.
there will be vector sign and no square on the last term
 
Thank you. Stevendaryl's suggestion is a good one, give it a try and let us know how you get along. The goal of that kind of substitution is to get a Hamiltonian which separates into a sum two Hamiltonians, one in the ##R## coordinate and the other in the ##r## coordinate.
 

Thread 'Please tell me where I am going wrong in this integral'

##|\Psi|^2=\frac{1}{\sqrt{\pi b^2}}\exp(\frac{-(x-x_0)^2}{b^2}).## ##\braket{x}=\frac{1}{\sqrt{\pi b^2}}\int_{-\infty}^{\infty}dx\,x\exp(-\frac{(x-x_0)^2}{b^2}).## ##y=x-x_0 \quad x=y+x_0 \quad dy=dx.## The boundaries remain infinite, I believe. ##\frac{1}{\sqrt{\pi b^2}}\int_{-\infty}^{\infty}dy(y+x_0)\exp(\frac{-y^2}{b^2}).## ##\frac{2}{\sqrt{\pi b^2}}\int_0^{\infty}dy\,y\exp(\frac{-y^2}{b^2})+\frac{2x_0}{\sqrt{\pi b^2}}\int_0^{\infty}dy\,\exp(-\frac{y^2}{b^2}).## I then resolved the two...
View full post »

Thread 'Direction of the magnetic field of an oscillating charge'

Hello everyone, I’m considering a point charge q that oscillates harmonically about the origin along the z-axis, e.g. $$z_{q}(t)= A\sin(wt)$$ In a strongly simplified / quasi-instantaneous approximation I ignore retardation and take the electric field at the position ##r=(x,y,z)## simply to be the “Coulomb field at the charge’s instantaneous position”: $$E(r,t)=\frac{q}{4\pi\varepsilon_{0}}\frac{r-r_{q}(t)}{||r-r_{q}(t)||^{3}}$$ with $$r_{q}(t)=(0,0,z_{q}(t))$$ (I’m aware this isn’t...
View full post »

Thread 'Initial conditions for orbits around a wormhole'

Hi, I had an exam and I completely messed up a problem. Especially one part which was necessary for the rest of the problem. Basically, I have a wormhole metric: $$(ds)^2 = -(dt)^2 + (dr)^2 + (r^2 + b^2)( (d\theta)^2 + sin^2 \theta (d\phi)^2 )$$ Where ##b=1## with an orbit only in the equatorial plane. We also know from the question that the orbit must satisfy this relationship: $$\varepsilon = \frac{1}{2} (\frac{dr}{d\tau})^2 + V_{eff}(r)$$ Ultimately, I was tasked to find the initial...
View full post »

Similar threads

Continuity Equation for a Dimensionless Harmonic Oscillator
Replies
16
Views
2K
Quantum Harmonic Oscillator, what is #E_0#?
Replies
5
Views
2K
Working out harmonic oscillator operators at ##L \rightarrow \infty##
Replies
11
Views
2K
A particle of mass 'm' is initially in a ground state of 1- D Harmonic oscillator potential V(x)....
Replies
3
Views
5K
Quantum Harmonic Oscillator with Additional Potential
Replies
1
Views
2K
Perturbation from a quantum harmonic oscillator potential
Replies
2
Views
2K
Operator that commutes with the Hamiltonian
Replies
3
Views
2K
What Parameter Should Be Used in Variational Approximation for This Hamiltonian?
Replies
1
Views
1K
2D isotropic quantum harmonic oscillator: polar coordinates
Replies
3
Views
6K
Ground state energy of harmonic oscillator
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top