seanster1324
- 8
- 0
Homework Statement
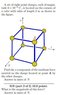
I attached a picture to make it easier...
Homework Equations
Coulomb's Law: F=k(q1*q2)/(r)^2
a^2+b^2=c^2
Charge properties
The Attempt at a Solution
I uploaded a picture of one of the cleaner sheets of work I used so far...Basically, I suppose I'm at a loss at figuring out where to start, and where to finish. I thought I was on the right track by calculating the magnitude of each charge affecting the vertex A, but apparently it hasn't got me very far.