A bar subject to a rolling disk which is released on an inclined plane

[Telemachus]

Homework Statement

I have this other exercise rigid in the plane, with which I am having problems.

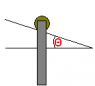
The rod of mass m and length l, is released based on the vertical position of rest with the small roller end A resting on the slope. Determine the initial acceleration A.

(neglect friction and mass of the roller A)

The answer given by the book is $$a_A=\displaystyle\frac{g\sin \theta}{1-\frac{3}{4}\cos^2\theta}$$

Homework Equations

I try to raise the moment equation, and Newton. But not me, not that I'm doing wrong. For this consider that the bar rotates about its center of mass.
$$I_{cm}=\displaystyle\frac{mL^2}{12}$$
$$N-mg\cos\theta=0$$
$$mg\sin\theta=ma_{cm}$$
$$I_{cm}\alpha=\displaystyle\frac{L}{2}mg\sin\theta\cos\theta$$

The Attempt at a Solution

$$\alpha=\displaystyle\frac{6g\sin\theta\cos\theta}{L}$$
$$a_cm=g\sin\theta$$

Then: $$a_A=a_{cm}+\displaystyle\frac{L}{2}\alpha=g\sin\theta+3g\cos\theta\sin\theta$$

Greetings and thanks for posting.

 

[Telemachus]

Should I post this on advanced physics?