A circuit problem from Thevenin's theorem (I cant work Vth out)

[Toyona10]

Homework Statement

Greetings to all,

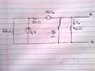
I can't work the Vth out (across terminals a and b) from the circuit in the image I've attached here.
There was a hint in the question too:' ... Define the voltage at the left most node as 'v', and write 2 nodal equations with Vth as the right node voltage'. The answer for Vth given in the book is 30V.

Homework Equations

The Attempt at a Solution

I've tried according to the hint given but my answer didn't match. Maybe there is a mistake with my nodal equations...? This is what I came up with:

For node a: 'v'= ir= 60*4= 240V

For node b: Vth/80 + Vth/40...= 0 --------> (1)

and Vth/40 = i delta ----->(2)

Yeah I know that in the 1st equation I didnt include a term for the 20Ω resistor as I'm not sure about how to because of the dependent voltage source in between (and when I somehow did, I got weird answers :S). So, I'd appreciate it very much if anyone would kindly show me the correct set of nodal equations I need to construct to get the correct answer for Vth.

Thank you c:

 

[NascentOxygen]

I'm not sure, but isn't that a dependent current source? It looks like it pumps current into the 60 ohm resistor, adding to the 4A.

See that node at the top of the 40 and 80 ohm resistors? There is 161.i (delta) flowing out of that node, so there must be an identical current, 161.i (delta) flowing into the node, and with terminals a-b being open, the only path for current to flow into the node is via the 80 ohms. So that tells you the current flowing in the 80 ohm resistor. (It also tells you the direction, because the sum total of all currents into a node must equal zero.)

 

[gneill]

I'm not sure, but isn't that a dependent current source? It looks like it pumps current into the 60 ohm resistor, adding to the 4A.

Looks like the symbol for a controlled voltage source. If it were a current source I'd expect to see and arrow inside it rather than the +/-.

As a hint, I might suggest first turning the 4A current source and its parallel resistance into its Thevenin equivalent.

 

[Toyona10]

I'm not sure, but isn't that a dependent current source? It looks like it pumps current into the 60 ohm resistor, adding to the 4A.

See that node at the top of the 40 and 80 ohm resistors? There is 161.i (delta) flowing out of that node, so there must be an identical current, 161.i (delta) flowing into the node, and with terminals a-b being open, the only path for current to flow into the node is via the 80 ohms. So that tells you the current flowing in the 80 ohm resistor. (It also tells you the direction, because the sum total of all currents into a node must equal zero.)

lol sorry that it isn't clear but that's a dependent voltage source, not a dependent current source...

 

[Toyona10]

Looks like the symbol for a controlled voltage source. If it were a current source I'd expect to see and arrow inside it rather than the +/-.

As a hint, I might suggest first turning the 4A current source and its parallel resistance into its Thevenin equivalent.

Yup, that's right, it is a dependent voltage source... and I converted the source as you suggested but now what? My main problem is how will I use the dependent voltage source in my nodal equations...because the way I tried to use it is incorrect as my answer doesn't match :S

 

[NascentOxygen]

If you want to get everything in terms of output voltage, then start by expressing i delta in terms of vth. That is, express the current through the 40 ohm resistor in terms of the voltage across it.

Oh, I see you have that already in your first post. Good.

So now you can state the voltage on the left side of the dependent voltage source. Again, state it in terms of vth.

 

[NascentOxygen]

The answer for Vth given in the book is 30V.

That's my answer, too.

For node b: Vth/80 + Vth/40...= 0 --------> (1)

It's now time to fix this equation. There are 3 currents associated with that node. You addressed two, and probably view them as leaving the node, so you can say the current flowing into the node must come from the dependent voltage source, emerging from its - terminal. You don't have to choose these directions, but once you settle on them you have to stay with them.

You can now write the current through the dependent voltage source in terms of vth.

When you get to here, you have both the voltage and current of the dependent voltage source in terms of vth.