lando45
- 84
- 1
A 0.50 kg glider on an air track is pulled along frictionlessly by a tensile force arising from a hanging 19.0 N weight. Over what distance will it travel in order that 14.0 J of work be done on it?
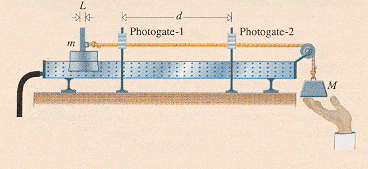
I've been set this question by one of my Physics teachers and it's got me a little confused...I conducted some research, and I think that the tensile is the force used to accelerate both masses, not just the hanging one. So do I need to find the acceleration it produces? Then I can find the force on the 0.50kg mass, and could consequently find the distance traveled from the given work done...but I don't know if this is right, and if it is, how I go about doing it! Many thanks.
I've been set this question by one of my Physics teachers and it's got me a little confused...I conducted some research, and I think that the tensile is the force used to accelerate both masses, not just the hanging one. So do I need to find the acceleration it produces? Then I can find the force on the 0.50kg mass, and could consequently find the distance traveled from the given work done...but I don't know if this is right, and if it is, how I go about doing it! Many thanks.