A prime limit that seems to approach a constant

[robnybod]

Ok here's the problem:

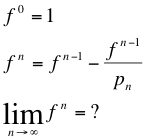
Using wolfram the first 100 results are these
heres a plot of a couple points
As you can see it doesn't seem to be approaching exactly zero, even though its very similar to 1/x (exactly the same if you replace P_n with just n)
Is there any way to prove whether this does approach 0 or some constant, or is it possible to make a program to approximate it to some extremely large n, to see if its approaching zero or some constant.

Thanks in advance, and sorry if the answer is obvious

 

[tiny-tim]

welcome to pf!

hi robnybod! welcome to pf!

it's decreasing and positive, so it must have a limit

to find the limit, use the usual trick of putting f_n = f_n-1

 

[robnybod]

Thank you!
so according to that it would go to zero, correct? because than f=f(1-1/P(n)) and f goes away, so you're left with -1/P(infinity)=0, which checks

 

[tiny-tim]

so according to that it would go to zero, correct?

correct!

(the reaoning isn't rigorous, but the result is ok)

 

[Norwegian]

Good morning,

Your infinite product ∏(1-p_i^-1), over all primes, does indeed converge to zero, but no f_n=f_n-1 trick is close to showing why.

The standard elementary proof here is to rewrite your limit as (Ʃ1/n)^-1 over the positive integers realizing that your limit is an euler product (google, wiki).

Note btw that if you add an exponent s to all your primes, your limit equals ζ(s)^-1, where ζ(s) is the Riemann zeta function, known to converge for all s>1 (and giving you non-zero limit in this case).

 

[atomthick]

Another proof would be to think of function f^k as being the probability to pick a natural number that has a factor among all the prime numbers except the first k prime numbers.

f⁰ = 1, the probability to pick a number that has a factor among all primes is 1
f¹ = f⁰ - f⁰/p₁, the probability to pick a number that has a factor among all prime numbers except the first prime is 1/2

at infinity this translates into

lim _{n->\infty}fⁿ = 0 because f^\infty is the same as asking what is the probability to pick a natural number that doesn't have a factor among all the prime numbers. Of course all natural numbers have a prime factor or are prime numbers therefore the answer is 0.