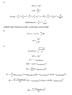A question about central-force movement

  • Thread starter Thread starter sapz
  • Start date Start date
  • Tags Tags
    Movement
Click For Summary
SUMMARY

The discussion centers on a physics problem involving a particle influenced by a central force defined as F(r) = -Ar^3 (r-hat). Participants analyze the effective potential, determine conditions for circular motion, and calculate the frequency of oscillations around a specific radius. Key insights include the necessity of incorporating centripetal acceleration in calculations and identifying algebraic errors that affect the final results. The particle cannot reach r=0 due to the nature of the effective potential.

PREREQUISITES
  • Understanding of central force dynamics
  • Familiarity with effective potential energy concepts
  • Knowledge of circular motion and centripetal acceleration
  • Ability to analyze asymptotic behaviors in mathematical functions
NEXT STEPS
  • Study the derivation of effective potential in central force problems
  • Learn about the conditions for circular motion in classical mechanics
  • Explore the concept of small oscillations and their frequencies
  • Review common algebraic errors in physics problem-solving
USEFUL FOR

Students and educators in physics, particularly those focusing on classical mechanics and central force motion, will benefit from this discussion.

sapz
Messages
33
Reaction score
1

Homework Statement



Hi there! Could you please help me with this question? Am I doing it right?

A particle is moving under a force of the form F(r) = -Ar^3 (r-hat). The particle begins its movement at a distance r0 and velocity v0.

A. Find and draw the effective potential. Can the particle arrive at r=0?
B. Find the velocity v0 so that the particle will move in a circle.
C. What is the frequency of the small movements (w0) around that radius?

Homework Equations





The Attempt at a Solution


The attempt is attached as an image.
 

Attachments

  • p111.png
    p111.png
    16.4 KB · Views: 525
Physics news on Phys.org
To sketch the graph, determine the asymptotic behaviours as r tends to 0, infinity, and find any local maxima and minima. Can it reach r = 0?
In B, you made an algebraic error going from the first line to the second. This propagated into your work in C.
In C, you left out centripetal acceleration in the second equation.
 
Thanks!
 

Similar threads

Finding the movement equation (non intertial system)
  • · Replies 1 ·
Replies
1
Views
1K
Circular Motion Problem: Particle Velocity and Acceleration Calculation
  • · Replies 18 ·
Replies
18
Views
2K
Function for the movement of a charged particle in a B field
  • · Replies 3 ·
Replies
3
Views
1K
Calculating Particle Speed with Velocity-Dependent Force
  • · Replies 1 ·
Replies
1
Views
3K
Problem in central force motion
  • · Replies 4 ·
Replies
4
Views
2K
Horizontal propagated movement of mechanical wave
  • · Replies 1 ·
Replies
1
Views
1K
Tangential movement in a waterslide
  • · Replies 35 ·
2
Replies
35
Views
3K
Two particles moving in a central potential
  • · Replies 1 ·
Replies
1
Views
1K
Does ω0 = ωf when radius of circular motion changes?
  • · Replies 11 ·
Replies
11
Views
2K
Solving Part c of Repulsive Force Homework Problem
  • · Replies 2 ·
Replies
2
Views
2K