A question of kinematics involving a changing velocity vector

[Adesh]

Homework Statement

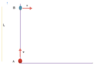
Point A moves uniformly with velocity v so that the vector v is continually "aimed" at point B which in its turn moves rectilinearly and uniformly with velocity u<v. At the initial moment of time v is perpendicular to u and the points are separated by a distance l. How soon will the points converge ?

Relevant Equations

distance = integral of velocity with time.

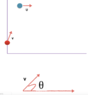
The statement "at the initial moment of time v ⊥ u and the points are separated by a distance l " gives us a picture like the one which I have added in attachment.
As the time passes velocity vector v would gradually change from fully vertical to fully horizontal in order to meet point B. Now, at any instant of time we have x-component of v as v cosθ and y-component as v sinθ. To catch point B our point A has to travel a distance of l in y- direction and to catch it in x-direction it has to cover the same distance as point B has covered. So, let's assume that they meet at time t , then

$$\int_{0}^{t} v cosθ dt $$ = ut

$$\int_{0}^{t} v sinθ dt $$ = l

Now, here I'm stuck. I know that θ is a function of time but I can't figure out which function is it. I know that x-component of v is gradually increasing sinusoidally and y-component is decaying sinusoidally but I'm not able to solve after that. I want to how can I solve for t after I have got those two equations.

 

[haruspex]

Think about how each velocity affects the distance apart.

 

[Adesh]

Think about how each velocity affects the distance apart.

Can you please elaborate just a little more?

 

[haruspex]

Can you please elaborate just a little more?

In a short period of time, dt, by how much does the motion of B change the distance between them?

 

[Adesh]

In a short period of time, dt, by how much does the motion of B change the distance between them?

I’m sorry but

In a short period of time, dt, by how much does the motion of B change the distance between them?

I’m sorry but I’m unable to use your clue.
If at any arbitrary time t we have velocities :- vcos$$\theta$$. , vsin$$\theta$$. and u.
So, distances are given by multiplying each instantaneous velocity by dt but I’m unable to keep track of l. How to write instantaneous distance in terms of l?
Please illustrate your clue.
Thank you.

 

[haruspex]

I’m sorry but

I’m sorry but I’m unable to use your clue.
If at any arbitrary time t we have velocities :- vcos$$\theta$$. , vsin$$\theta$$. and u.
So, distances are given by multiplying each instantaneous velocity by dt but I’m unable to keep track of l. How to write instantaneous distance in terms of l?
Please illustrate your clue.
Thank you.

Don't work in terms of velocity components in the fixed XY frame. That just confuses things.
In time dt B moves distance udt to some location B'. What, roughly, is the angle ABB'?

 

[Adesh]

Don't work in terms of velocity components in the fixed XY frame. That just confuses things.
In time dt B moves distance udt to some location B'. What, roughly, is the angle ABB'?

Is angle ABB' going to be 90 degrees?

 

[haruspex]

Is angle ABB' going to be 90 degrees?

Right. So how much does the distance udt that B moves affect its distance from A?

 

[archaic]

you need a good sketch.

Where $\Delta l$ represents the decrement in the distance between both points.
I added the $-$ sign before $?_2$ because it is decreasing the distance.
Do not get discouraged by the problems in Irodov's book, they're not easy.You'll nurture the intuition for these kind of problems where you need to seek out how the distance or whatever is changing. The problem before it (1.12) can be solved the same way, you need to find how the distance between two points is changing.

 

[Adesh]

The model, which I have gained from your answer, is like this

but the problem is I'm not able to tell what A'B' would be? This is because at an arbitrary time I can't tell what AB is? Even if I use the information provided by haruspex that angle ABB' is roughly 90 degrees then also how can I solve for A'B'?
I want to thank you for giving me some attention, I'm really grateful to you. You know there are solutions present on internet (https://crackthequestion.blogspot.com/2008/06/q-113-in-general-physics-by-ie-irodov_20.html) but the problem is that they are using relative velocity concept (the component of u in the direction of v) just for the sake of solution, there is ground for doing it. What we should do is to take the component of v in the direction of u, but this approach is failing to give the answer. I really thank you for giving me your precious time, I earnestly request you to help through this question.

 

[ehild]

View attachment 247043

The model, which I have gained from your answer, is like this
but the problem is I'm not able to tell what A'B' would be?

Do not want to determine the positions at an arbitrary time. Think of displacements in very short time interval dt, and the component of the displacements in the direction of the line connecting A and B. You want to make that distance zero, that is why you need those components.
It is clear that motion of A diminishes the distance r between A and B by vdt. How much does the motion of B change the distance r in dt time? See the orange triangle.The velocity
vectors u and v enclose the angle theta, the same angle, v makes with the horizontal.

 

[haruspex]

but the problem is I'm not able to tell what A'B' would be?

I was careful to ask, first, about the distance AB', not A'B'. And it will help if you draw the 90 degree angle more accurately.