A revolving tetherball vs. a spinning top

[kmarinas86]

Diagram:

Text from the diagram:
____________

So, where does that force (?) come from?

There is no known force allowing the gravity directed to the ground to pull an unspun top toward the principal axis, as such is a horizontal force (orthogonal to this axis), unlike the vertical force of gravity, which cannot be the cause of this. When the top is not spinning, any horizontal force (friction) the ground that may apply opposite to the reactive centrifugal force would only cause the upper end of the top to tilt AWAY from the principal axis and toward parity with the ground.

Yet, we INFER from a spinning top that a horizontal force must exist on it towards the principal axis, as we inferred that a force must exist on the tetherball, as required by the conservation of momentum.

It is as if the cross product of top spin angular momentum and the precessional frequency CREATED the torque strength of an “anchor”. (IS THIS THE ANSWER TO THE ?)
____________

 

[Simon Bridge]

"A spinning top in upside-down land" ... what does this mean? Gravity is up?

Looks like a top spinning in place, at an angle, and precessing.
The descriptions of both the tether ball and the top appear to be mixing up inertial and non-inertial representations. It's trying to use an analogy that does not quite apply since the top has an additional angular momentum term not present in the tether-ball.

Try repeating the analysis entirely in an inertial frame.

The physics of both tether balls and tops are well established - have you tried looking them up?Where did you get this graphic?

 

[kmarinas86]

"A spinning top in upside-down land" ... what does this mean? Gravity is up?

Looks like a top spinning in place, at an angle, and precessing.
The descriptions of both the tether ball and the top appear to be mixing up inertial and non-inertial representations. It's trying to use an analogy that does not quite apply since the top has an additional angular momentum term not present in the tether-ball.

No. I am not trying to assert equivalence between the top and the tetherball. I actually am trying to disestablish the notion that the same arguments that apply to the functioning of a tetherball could somehow totally account for the behavior of a top, that somehow that all you need conservation of angular momentum, and that after you assume that, it all somehow handy-dandy, as if you identified the balance of forces required by Newton's law, as well as their origins. What I am saying in the diagram is that the balance of forces is easy to see for the case of the tetherball, but it is not easy to see in the case of the top. Conservation of momentum is insisted upon by the diagram, not doubted. Yet, as the diagram suggests, there does not seem to be an object outside the top that is actually providing the rotating force on the top toward alignment with the principal axis. The ground is not doing this and gravity is not doing this (and in fact gravity, together with the influence of the ground, only provides the rotating force on the top away from alignment with the principal axis), as explained in the bottom of the diagram:

Try repeating the analysis entirely in an inertial frame.

Both frames ARE inertial. The viewer in these examples is situated in the non-rotating ground frame. The inertial viewer either sees a non-inertially moving tetherball or a non-inertially moving top. None of these spinning motions are being evaluated from a spinning frame of reference.

The term "reactive centrifugal force" does not refer specifically to a spinning frame of reference. It has a definition which is applicable in inertial frames as well:

Reactive centifugal force
Fictitious centifugal force
Fictitious vs. reactive centifugal force

I hope that makes it clearer.[/color]

http://en.wikipedia.org/wiki/File:Reactive_centrifugal_and_centrifugal_forces.PNG

The physics of both tether balls and tops are well established - have you tried looking them up?

I have done so many, many, MANY times.

Where did you get this graphic?

https://www.physicsforums.com/attachment.php?attachmentid=43215&stc=1&d=1327758376

 

[kmarinas86]

I found my mistake. I kept on putting principal axis at the location of the fulcrum, but that's not where it is actually supposed to be. Here is the corrected one, with the balance of forces revealed:

 

[Simon Bridge]

I actually am trying to disestablish the notion that the same arguments that apply to the functioning of a tetherball could somehow totally account for the behavior of a top, that somehow that all you need conservation of angular momentum, and that after you assume that, it all somehow handy-dandy, as if you identified the balance of forces required by Newton's law, as well as their origins.

I had thought you had found the graphic on the web someplace other than Physics Forums - I take it then, that this is your work?

The diagrams are unclear then - try tidying them up.

The way you have drawn them it looks, for example, like you intend the reactive centrifugal force to act on the body in curved motion. The free-body diagram for the ball shouldn't have it - it should only have tension and gravity. (Technically you have not drawn free body diagrams at all though so it is hard to see what you intend anyways.)

Your "corrected" diagram looks a little odd to me, you seem to be having the entire top moving in a circle - and you seem to have the reactive centrifugal force at the center of mass for the top (the body doing the circular motion) - compare real life example:
http://www.youtube.com/watch?v=03k9CgvL_dQ&feature=related
... the contact point sits still and the com precesses much like your first diagram appears to be showing: axis through the point.

I don't see any torques or angular momenta in your diagram - which would seem to be needed if you really want to show what else, besides conservation of angular momentum, is needed to identify and locate all the forces.

Try modelling this situation:
http://www.youtube.com/watch?v=8H98BgRzpOM&feature=related

The torque causing the rotation comes from gravity.
This you should know from your copious reading of the physics of the spinning top.
eg. You will have read this demo... it describes the relationship between gravity, spin angular momentum, and precession angular momentum. But you want something more mathematical. But you must have found this gyroscope physics guide which shows (4th figure down) the kind of free body diagram you need to analyze the top in terms of angular momentum - the analysis follows - the site includes a fbd analysis of the wheel too.

So what is the problem?

 

[kmarinas86]

"

I had thought you had found the graphic on the web someplace other than Physics Forums - I take it then, that this is your work?

The diagrams are unclear then - try tidying them up.

The way you have drawn them it looks, for example, like you intend the reactive centrifugal force to act on the body in curved motion. The free-body diagram for the ball shouldn't have it - it should only have tension and gravity. (Technically you have not drawn free body diagrams at all though so it is hard to see what you intend anyways.)

Your "corrected" diagram looks a little odd to me, you seem to be having the entire top moving in a circle - and you seem to have the reactive centrifugal force at the center of mass for the top (the body doing the circular motion) - compare real life example:
http://www.youtube.com/watch?v=03k9CgvL_dQ&feature=related
... the contact point sits still and the com precesses much like your first diagram appears to be showing: axis through the point.

The axis is not exactly through the point. However, it is asymptotically close to it.

When the axis is exactly at the point of the fulcrum, then the torque due to gravity has been avoided as the top would be directly spinning vertically.

I don't see any torques or angular momenta in your diagram - which would seem to be needed if you really want to show what else, besides conservation of angular momentum, is needed to identify and locate all the forces.

Try modelling this situation:
http://www.youtube.com/watch?v=8H98BgRzpOM&feature=related

The torque causing the rotation comes from gravity.

The axis of the torque component that a "gravitational field" produces on the top is horizontal. Such a torque could tip over the Leaning tower of Pisa. A rotation from a vertical h direction towards horizontal r direction produces a torque vector in a horizontal phi direction perpendicular to both. The integral of such a torque with respect to angle gives us the amount of work that was done around that axis by the gravitational field. Integrating this torque, net of other torques, with respect time, would give us the angular momentum around such a axis, angular momentum that causes the top to rotate from vertical to horizontal.

However, the axis of the torque component that is needed to cause the top to accelerate around the principal axis is vertical. If gravity were really to cause that, then gravity would have to be a solenoidal field, different from a simple attraction between two masses.

In any case, I thought the torque causing the rotation comes only from the initial spinning of the top. The gravity only causes a tilt in the axis. At some point a "tug-of-war" angle is established between gravity and the precessing top.

Even in my second diagram, all the top can do in terms of the friction is to push the Earth beneath the top away from the principal axis.

As suggested by this diagram, at some point, the gravitational torque must be canceled by a torque similar to what could cause a cause race car to flip over on a turn that is not banked properly. Therefore, the part of top opposite from the ground's contact must lean towards the principal axis if it is to lean at all.

This you should know from your copious reading of the physics of the spinning top.
eg. You will have read this demo... it describes the relationship between gravity, spin angular momentum, and precession angular momentum. But you want something more mathematical. But you must have found this gyroscope physics guide which shows (4th figure down) the kind of free body diagram you need to analyze the top in terms of angular momentum - the analysis follows - the site includes a fbd analysis of the wheel too.

So what is the problem?

Note that point P is treated as a frictionless pivot. Therefore it exerts no moment (torque) on the rod.

If we treat the top and the ground as an isolated system, then we can assume that there is no net force on the Earth and the top. The Earth must produce a force equal and opposite to the top so that the center of mass can remain fixed with respect to the initial center of mass frame, and that is a very important requirement to obey the law of conservation of momentum.

The wrong thing to do was to assume that a top precessing at an angle can have its principal axis going exactly though its fulcrum.

 

[Ken G]

When the axis is exactly at the point of the fulcrum, then the torque due to gravity has been avoided as the top would be directly spinning vertically.

I believe this is your key mistake. First of all, there's no need for sideways friction-- the top would work fine on ice, though it would precess so as to keep its center of mass in the same place, so the fulcrum would go in a circle. There is no need for any horizontal forces, the basic reasons for precession are the same-- which is that the point gravity acts (the center of mass) is not directly above the point where the upward force from the ground acts (the fulcrum), and so we have torque and a rate of change of angular momentum. If you want to keep the fulcrum in place, you do need a sideways force from the ground, and that will be a net force (unbalanced) on the system. You can, if you insist, use the awkward notion of a "reactive centrifugal force", but this is not a real force it is a fictitious force similar to using a noninertial reference frame.

 

[kmarinas86]

I believe this is your key mistake. First of all, there's no need for sideways friction-- the top would work fine on ice

Ice is not frictionless. Just look at the skate marks that are formed in a skating rink. A lot of friction occurs between layers of ice as opposed to between the ice and the skates. This friction crushes the crystal structure of the ice, forming a water layer between the skates and the ice.

, though it would precess so as to keep its center of mass in the same place, so the fulcrum would go in a circle.

In an isolated system, the center of mass should move inertially, or not at all. A center of mass that moves non-inertially requires a force external to that system.

I consider that the ice+earth and the top can be treated as a one isolated system. If the top accelerates toward the central axis, then the ice must be the reaction to that action. Perhaps there is a reason why you might disagree with that. To have ice be a reaction mass implies friction. I don't believe in reactionless drives, and I don't believe in coupling without traction, and traction is a kind of friction, though we must not confuse the force of friction with heat losses. Tires have traction, but when they lose it they actually produce more heat losses because the power is used in creating a lot of displacement between frictioning surfaces, such as when you burn out a tire. Without this displacement, you instead cause rotation of the tires without slippage which doesn't produce nearly as much heat loss compared to burning them out.

There is no need for any horizontal forces, the basic reasons for precession are the same-- which is that the point gravity acts (the center of mass) is not directly above the point where the upward force from the ground acts (the fulcrum), and so we have torque and a rate of change of angular momentum.

If a nut is screwed onto a threaded bolt, and if I turn the wrench to tighten that nut, the torque axis is aligned with the threaded bolt. That threaded bolt is not going to be perpendicular to that torque axis. Similarly, if I spin a wheel, it is not equivalent to pivoting the wheel to the left. Nobody here but me has yet to talk about the orientation of the torque axis. I think that is an example of systematic avoidance of an issue.

Angular momentum is a vector. It is the result of integrating torque with respect to time. Torque is also a vector. The angular momentum vector component that results from projecting that vector onto the principal axis is perpendicular to the torque vector due to gravity. The integration of the torque vector with respect to time creates an angular momentum vector parallel to that torque vector. If the object moves through space, we can consider instantaneous torque and instaneous changes of angular momentum. Without the principal spin of the top, gravity does exactly what we expect it to do. However, by doing work by the integration of a vertical torque vector with respect to angle, we somehow create a horizontal torque vector as well.

For every precessing torque, there must be opposite complement to this, and that follows directly from Newton's laws for an inertial reference frame. That precessing torque is not only required to conserve angular momentum, but its origins must be understood. For example, after the force causing the top to accelerate to a certain steady state spin is removed, you can treat the ground and the top as being an isolated system, that is to say, isolated from the original actor that caused the top to move the way it did. No longer could you say that when the top continues to precess thereafter that the torque on the top that prevents it from tipping over is still being provided by the original actor. The precessing torque persists even in the absence of any further supplied torque outside the system combining both the top and the ground. If the torque of gravity were to have no equal or better match in the tug-of-war with the top, it will succeed in tipping over the top. Of course, the ground would slightly rotate toward the top as well though this movement is negligible given the much greater mass the ground has compared to the top. If the top were made to actively accelerate using its own source of energy, it can actually upright itself against gravity, but only if there is another mass to interact with. For the top, this mass is a ground. For other systems, the mass is a pulley, although in most examples this pulley is ultimately connected somehow to the ground.

If you want to keep the fulcrum in place, you do need a sideways force from the ground, and that will be a net force (unbalanced) on the system.

You chose to not make it clear what the system is. Is it the top and the ground, or just the top? Not making this clear is awkward for me.

In any case, what you are talking about is not a closed system, as having an unbalanced force requires an external body in order to explain this lack of force equilibrium, and that must be an external body that you are ignoring.

I don't believe in reactionless drives, reactionless acceleration, or reactionless expansion.

You can, if you insist, use the awkward notion of a "reactive centrifugal force", but this is not a real force it is a fictitious force similar to using a noninertial reference frame.

There is a ficitious component to it and a non-fictitious component to the reactive centrifugal force. The non-fictitious component is what remains when we choose an inertial frame, which is the entire strategy I have used in my diagram, as no non-inertial frame has been chosen for any observers.

The diagram I showed from wiki, which illustrates both cases, proves my point:

http://en.wikipedia.org/wiki/File:Reactive_centrifugal_and_centrifugal_forces.PNG

 

[Ken G]

Ice is not frictionless.

If you are not familiar with the device of using idealizations in physics, that would be a good place to begin learning how physics works. The point about the top is that there is nothing about friction that is necessary to understand the basic laws at play in the precession of a top.

In an isolated system, the center of mass should move inertially, or not at all. A center of mass that moves non-inertially requires a force external to that system.

Yes, as it does for both the tetherball and the top (with friction) that you indicated in your diagram. Again: your diagram is of a system that is not moving inertially, and is not an isolated system. Hence, you should not expect there to be a force balance, nor is there a force balance. It is not recommended to invoke the notion of a reactive centrifugal force, but if you understand what you are doing, it isn't wrong. As I said, it is quite similar to working in a noninertial reference frame in which the top is not moving, only spinning in place.

I consider that the ice+earth and the top can be treated as a one isolated system.

So you think you want to include the center of mass in your diagram? I don't think you want to do that. It makes a lot more sense, and is much more standard, to treat the top as not an isolated system, but rather as a system with a force from the ground, and a force from gravity, acting on it. If we use frictionless ice, we will find all the forces balance, and the center of mass of the top is not accelerating, but it is still not an isolated system. If you use your diagram, then there is a net force (dump the reactive centrifugal force), it is horizontal, and it makes the center of the top go around in a circle. Either way, the spin axis goes around in a circle due to the torque, and that is called precession.

If the top accelerates toward the central axis, then the ice must be the reaction to that action.

That is essentially nonsense, and is not likely to help you make correction calculations or predictions about the motion of the top. That way of thinking is likely to find you coming to a physics forum to help you understand why your understanding and predictions are not working out, which is just what you should do-- so listen to the answers you receive here.

For every precessing torque, there must be opposite complement to this, and that follows directly from Newton's laws for an inertial reference frame.

This is just more nonsense, it's not language that is going to help you understand anything, or make any correct predictions. It just isn't, you will not get the answers right if you try to think in this awkward and unreliable way. An inertial frame is just the frame of the observer regarding the top, it is not the frame of the top so it has nothing to do with the forces or torques on the top. An observer in an inertial frame does not require there to be any complement to torque on the top, because the top is not an isolated system (the complement is a torque on the Earth, whose impact is not being tracked expressly because we can depend on the Earth to act in a way that is unimpressed by this torque). And you are definitely not regarding the top and the Earth as a combined isolated system, as there is nothing interesting happening to that isolated system. What is interesting is what is happening to the top, which is not isolated.

That precessing torque is not only required to conserve angular momentum, but its origins must be understood.

More confusing and awkward thinking. Precession is not an example of conservation of angular momentum, it is an example of a rate of change of angular momentum due to nonzero torque. It is true that the system including the Earth does conserve angular momentum, but the conservation of the angular momentum of that system does not tell you anything useful about the precession of the top, expressly because the motion of the Earth is being counted on to not be influenced in any way by the top. This is pretty much the whole purpose of attaching the top to the Earth in the problem.

You chose to not make it clear what the system is. Is it the top and the ground, or just the top?

It is just the top. There would never be the slightest good reason to make the system be the top and the ground, if you want to understand tops. The only thing you need the ground to do is not move.

 

[kmarinas86]

"Ice is not frictionless."

If you are not familiar with the device of using idealizations in physics, that would be a good place to begin learning how physics works. The point about the top is that there is nothing about friction that is necessary to understand the basic laws at play in the precession of a top.

"In an isolated system, the center of mass should move inertially, or not at all. A center of mass that moves non-inertially requires a force external to that system."

Yes, as it does for both the tetherball and the top (with friction) that you indicated in your diagram. Again: your diagram is of a system that is not moving inertially, and is not an isolated system.

The parts of the systems (ground/Earth PLUS top or tetherball) described do not move inertially, but is the OBSERVER that is inertial. The system is EVALUATED from an INERTIAL, NON-ROTATING frame.

Just because you have two objects moving non-inertially DOES NOT mean that the combined mass moves non-inertially, which we can call a center of mass.

We could say that the tetherball and the ground gyrate in opposite directions in this frame with respect to the principal axis.

The ground does not "rotate" in this frame, but it gyrates, like a hydraulic powered Earthquake-simulating platform, square in shape, making circular, horizontal maneuvers, with respect an external observer, so this doesn't contradict my earlier statement about the ground's lack of rotation.

Hence, you should not expect there to be a force balance, nor is there a force balance.

The torque external to the top is not torque external to the system if we include the ground/Earth.

Tell me what do YOU call the closed system then in which angular momentum is conserved? I'd like to know what you think about that.

It is not recommended to invoke the notion of a reactive centrifugal force, but if you understand what you are doing, it isn't wrong. As I said, it is quite similar to working in a noninertial reference frame in which the top is not moving, only spinning in place.

Similar, but not equivalent.

"I consider that the ice+earth and the top can be treated as a one isolated system."

So you think you want to include the center of mass in your diagram? I don't think you want to do that. It makes a lot more sense, and is much more standard, to treat the top as not an isolated system, but rather as a system with a force from the ground, and a force from gravity, acting on it.

THAT IS THE ISOLATED SYSTEM: ice+earth+top, OR equivalently, ground+top.

If we use frictionless ice, we will find all the forces balance, and the center of mass of the top is not accelerating, but it is still not an isolated system.

Of course the top is not an isolated system. A precessing object must have at least one complementary object to explain its behavior.

If you use your diagram, then there is a net force (dump the reactive centrifugal force), it is horizontal, and it makes the center of the top go around in a circle.

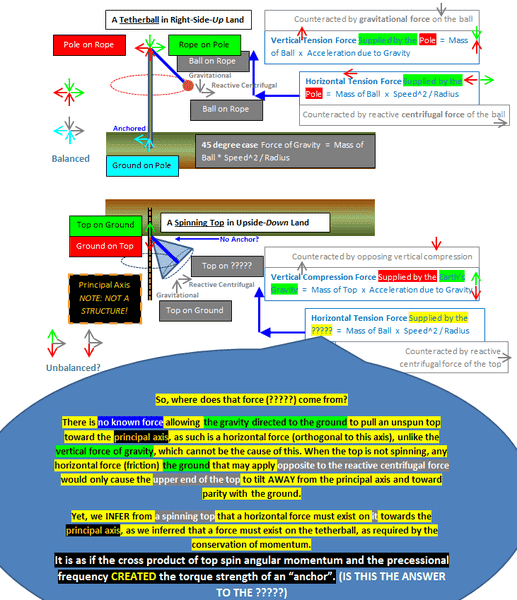
As far as the diagram I showed is concerned, the reactive centrifugal force when evaluated from an INERTIAL frame is identical to the horizontal tension force on the central mass of the rope+ball by the peripheral masses on the rope+ball. In this sense, "reactive centrifugal force" is what prevents the radial distance from the principal axis from decreasing.

Either way, the spin axis goes around in a circle due to the torque, and that is called precession.

Sure.

"For every precessing torque, there must be opposite complement to this, and that follows directly from Newton's laws for an inertial reference frame."

That is essentially nonsense, and is not likely to help you make correction calculations or predictions about the motion of the top. That way of thinking is likely to find you coming to a physics forum to help you understand why your understanding and predictions are not working out, which is just what you should do-- so listen to the answers you receive here.

Torque is the derivative of angular momentum with respect to time.

The system angular momentum must be computed with respect to a point. That means for every mass with a velocity, one must draw a radial vector from the point of evaluation and that mass in question and then take the cross product of that radial vector and the velocity of the mass and then multiply that by the scalar mass to get a vector. Adding those vectors up for a set of masses totaling that whole system gives us the total angular momentum of masses evaluated from that point.

If I have a closed system, there is no more external torque on that closed system. The torque and work done on a closed system by other systems is zero. In real life, this is of course is an approximation, as any real system can have external forces on them, even if those forces are orders of magnitudes less.

The momentum of the top is not conserved as we realize that the ground reacts with an opposite change in momentum as that experienced by the top. It is easy to consider the system as a whole to be closed when other forces on the top and the ground are negligible. So if the ground and the top combine to form an isolated system, then the angular momentum of THAT WHOLE THING is conserved, with the top and the ground independently subject to rotational non-equilbrium, while the system as a whole is not perturbed by significant external torques.

This is just more nonsense, it's not language that is going to help you understand anything, or make any correct predictions. It just isn't, you will not get the answers right if you try to think in this awkward and unreliable way. An inertial frame is just the frame of the observer regarding the top, it is not the frame of the top so it has nothing to do with the forces or torques on the top.

"it is not the frame of the top so"
"it has nothing to do with the forces or torques on the top"

Sure it does. An inertial frame is an inertial frame of reference against which you can evaluate non-inertial motions. For example. I can be moving inertially while making observations about a top's motions which are non-inertial. I don't have to be spinning with the top to see the top doing what it does. I don't have to be moving non-inertially to see non-inertial motion. Viewing non-inertial motion from a non-inertial frame just makes things more complicated. That's why I do not try to invoke a rotating observer. Viewing things from a non-inertial frame is simply awkward and such is not the way to determine the conservation of energy, momentum, angular momentum, in any case.

An observer in an inertial frame does not require there to be any complement to torque on the top, because the top is not an isolated system (the complement is a torque on the Earth, whose impact is not being tracked expressly because we can depend on the Earth to act in a way that is unimpressed by this torque).

And you are definitely not regarding the top and the Earth as a combined isolated system, as there is nothing interesting happening to that isolated system.

On the contrary, it is interesting to me, but it is not interesting to you. I have several times considered the top and the Earth as a combined isolated system in the limiting case of a spinning top. You object to this, insisting that the top is a "system".

What is interesting is what is happening to the top, which is not isolated.

What is interesting to me is the all the parts of the "system" taken together. I call this the system including all the objects that are involved in this calculation. Try getting the top to precess in Earth's gravity when it is in free-fall. How can the ground be ignored?

"That precessing torque is not only required to conserve angular momentum, but its origins must be understood."

More confusing and awkward thinking. Precession is not an example of conservation of angular momentum, it is an example of a rate of change of angular momentum due to nonzero torque.

" it is an example of a rate of change of angular momentum due to nonzero torque"...

...caused by one or more other objects that (axiomatically) constitute that system.

It is true that the system including the Earth does conserve angular momentum, but the conservation of the angular momentum of that system does not tell you anything useful about the precession of the top, expressly because the motion of the Earth is being counted on to not be influenced in any way by the top.

It is vanishingly small, but it is non-zero.

I, for one, cannot count on the Earth to not be influenced in any way by the top. The Earth is not a rigid particle.

This is pretty much the whole purpose of attaching the top to the Earth in the problem.

"You chose to not make it clear what the system is. Is it the top and the ground, or just the top?"

It is just the top. There would never be the slightest good reason to make the system be the top and the ground, if you want to understand tops. The only thing you need the ground to do is not move.

If I want to understand tops, I want to do so in the context of conservation of energy, momentum, and angular momentum. I don't care what anyone thinks about what's "not relevant" if the impact is non-zero. If I want to think about it, it's not useful to me to brush it off as something that shouldn't even be looked at.

 

[Ken G]

I, for one, cannot count on the Earth to not be influenced in any way by the top. The Earth is not a rigid particle.

And if you are happy about this degree of understanding, then I guess you have no problems. But then you also have no reason to post this thread. So if you do have problems, and you do find it difficult to get to the right answer to predictions for how systems will behave etc., then I'm telling you this is the source of your problem. Those who do understand tops quite well, and don't have trouble arriving at correct predictions about how they behave, invariably do treat the Earth as a rigid particle, and invariably don't treat the top+Earth system. They just treat the top, they treat it as a non-isolated system, they expect it to have a net force on it that causes its center of mass to precess in a circle, and above all, they expect it to have a net torque on it. They do not expect any of these effects to cancel out in any way, nor do they ever imagine the presence of any reactive centrifugal forces, or reactive torques. Those concepts are just not very useful, and will usually lead you into error. But again, if someone gives you something to calculate about a top, and you can get to the correct prediction, then you can do it your way. I suspect this will not be the case, hence your posting here.

If I want to understand tops, I want to do so in the context of conservation of energy, momentum, and angular momentum.

And I'm telling you that is not how you will understand tops, so if you have trouble understanding them, this is the reason. Those who do understand tops do not think of the relevant angular momentum as being conserved, because they are just thinking about the tops, and the angular momentum of the top is not conserved. Indeed, the single most important thing for understanding the motion of tops is to realize that the angular momentum of the top is not conserved, and the angular momentum of the top+Earth will never tell you anything interesting about tops. If you don't get this, you are just never going to get tops. I apologize if you think I'm being condescending, but all the same, what I'm telling you is the truth, and I imagine that's what you came here to hear.

 

[kmarinas86]

And if you are happy about this degree of understanding, then I guess you have no problems. But then you also have no reason to post this thread. So if you do have problems, and you do find it difficult to get to the right answer to predictions for how systems will behave etc., then I'm telling you this is the source of your problem. Those who do understand tops quite well, and don't have trouble arriving at correct predictions about how they behave, invariably do treat the Earth as a rigid particle, and invariably don't treat the top+Earth system. They just treat the top, they treat it as a non-isolated system, they expect it to have a net force on it that causes its center of mass to precess in a circle, and above all, they expect it to have a net torque on it. They do not expect any of these effects to cancel out in any way, nor do they ever imagine the presence of any reactive centrifugal forces, or reactive torques. Those concepts are just not very useful, and will usually lead you into error. But again, if someone gives you something to calculate about a top, and you can get to the correct prediction, then you can do it your way. I suspect this will not be the case, hence your posting here.And I'm telling you that is not how you will understand tops, so if you have trouble understanding them, this is the reason. Those who do understand tops do not think of the relevant angular momentum as being conserved, because they are just thinking about the tops, and the angular momentum of the top is not conserved. Indeed, the single most important thing for understanding the motion of tops is to realize that the angular momentum of the top is not conserved, and the angular momentum of the top+Earth will never tell you anything interesting about tops. If you don't get this, you are just never going to get tops. I apologize if you think I'm being condescending, but all the same, what I'm telling you is the truth, and I imagine that's what you came here to hear.

I never thought of it that way. Thank you for spending the time to explain that!

 

[Ken G]

Glad to help!