maverick_bih
- 1
- 0
This looks like an easy one, but I haven't found anyone yet who has answered it correctly, including me...
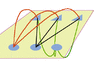
So, the goal is (like shown in the picture), to connect all three circles to each of the three triangles (nine connections in total, i have managed eight). Give it a try. You can go around the triangles and circles with the lines, just as long as they DON'T cross.
∆ ∆ ∆
O O O
So, the goal is (like shown in the picture), to connect all three circles to each of the three triangles (nine connections in total, i have managed eight). Give it a try. You can go around the triangles and circles with the lines, just as long as they DON'T cross.
∆ ∆ ∆
O O O
Last edited: