vstrimaitis
- 2
- 0
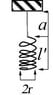
1. A cylindrical string is made out of thin wire.
- The distance between every loop of an unstretched spring is equal;
- The radius of every loop of the spring is r = 4 cm;
- The length of an unstretched spring is l = 20 cm;
- The mass of the spring is m = 50 g;
2.
- What is the constant of the spring (k)?
- What is the period of this system, if the angle, at which it is released, is small?
3. I haven't really solved any problems when the weight is not attached on the end of the spring. Does it work the same way or not? If it does, I'll be able to find k. But I have no idea what to do with the period... Any help at all would be appreciated ^^