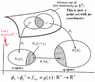
friend said:
I'm trying to reconcile these statements with others that say that the curvature cannot change with a change of coordinates, which would preclude a coordinate transform from flat to curved space.
It seems to me that it would be a straightforward procedure to prove that curvature is invariant wrt coordintate changes since we have:
The scalar curvature is
\[R = {g^{\sigma \nu }}{R_{\sigma \nu }}\]
where \[{R_{\sigma \nu }}\] is the Ricci tensor
\[{R_{\sigma \nu }} = {R^\rho }_{\sigma \rho \nu }\]
where \[{R^\rho }_{\sigma \mu \nu }\] is the Rieman curvature tensor
\[{R^\rho }_{\sigma \mu \nu } = {\partial _\mu }{\Gamma ^\rho }_{\nu \sigma } - {\partial _\nu }{\Gamma ^\rho }_{\mu \sigma } + ({\Gamma ^\rho }{_\mu _\lambda }{\Gamma ^\lambda }_{\nu \sigma } - {\Gamma ^\rho }{_\nu _\lambda }{\Gamma ^\lambda }_{\mu \sigma })\]
where \[{\Gamma ^\rho }_{\nu \sigma }\] is the Christoffel symbol
\[{\Gamma ^\rho }_{\nu \sigma } = \frac{1}{2}{g^{\rho \alpha }}(\frac{\partial }{{\partial {q^\sigma }}}{g_{\alpha \nu }} + \frac{\partial }{{\partial {q^\nu }}}{g_{\alpha \sigma }} - \frac{\partial }{{\partial {q^\alpha }}}{g_{\nu \sigma }})\]
where g is the metric tensor such that
\[{\rm{g = }}{{\rm{J}}^T}{\rm{J}}\]
where J is the jacobian
\[{\rm{J}} = \left[ {\begin{array}{*{20}{c}}<br />
{\frac{{\partial {q^1}}}{{\partial {x^1}}}}&{\frac{{\partial {q^1}}}{{\partial {x^2}}}}& \cdots &{\frac{{\partial {q^1}}}{{\partial {x^n}}}}\\<br />
{\frac{{\partial {q^2}}}{{\partial {x^1}}}}&{\frac{{\partial {q^2}}}{{\partial {x^2}}}}& \cdots &{\frac{{\partial {q^2}}}{{\partial {x^n}}}}\\<br />
\vdots & \vdots & \ddots & \vdots \\<br />
{\frac{{\partial {q^m}}}{{\partial {x^1}}}}&{\frac{{\partial {q^m}}}{{\partial {x^2}}}}& \cdots &{\frac{{\partial {q^m}}}{{\partial {x^n}}}}<br />
\end{array}} \right]\]
where \[{q^\mu } = {q^\mu }({x^i})\] is the coordinate transformation.
I'm thinking that if someone went through all the tedious partial derivatives they might prove that the scalar curvature is invariant, or at least under what conditions of the partials that it remains invariant. Has anyone seen such a proof ever worked out? Or would someone like to work it out? I'm not sure I have that much skill or patience. Thanks.