hojoon yang
- 8
- 0
Given a Gaussian process X(t), identify which of the following , if any, are gaussian processes.
(a)X(2t)
solution said that X(2t) is not gaussian process, since

and similarly
Given Poisson process X(t)
(a) X(2t)
soultion said that X(2t) is not poisson process, since same reason above.
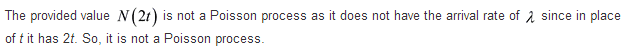
BUT
I think that in stochastic process, Time t is just constant value.
so I think X(2t), X(10000t), X(t+100) is also gaussian process ,or poisson process
doesn't care about whatever t is.
answer is?
(a)X(2t)
solution said that X(2t) is not gaussian process, since
and similarly
Given Poisson process X(t)
(a) X(2t)
soultion said that X(2t) is not poisson process, since same reason above.
BUT
I think that in stochastic process, Time t is just constant value.
so I think X(2t), X(10000t), X(t+100) is also gaussian process ,or poisson process
doesn't care about whatever t is.
answer is?