About the binding of O2 to Hemoglobin molecules

[samy4408]

TL;DR

the saturation of Hb related to its partial pressure

Hello, I just learned about the binding capacity of Hemoglobin (Hb) and that it is proportional to the partial pressure of O2 in the blood here is the curve :

it does have a sigmoidal shape, but here is the problem: in the lecture, it's said that Hb has an increasing affinity to O2 the more O2 is bound to it, isn't it the opposite since we have to put way more partial pressure to go from 80% to 100% saturation than to go from 0% to 20%.
hoping for a reply .thanks.

 

[Borek]

Hello, I just learned about the binding capacity of Hemoglobin (Hb) and that it is directly proportional to the partial pressure of O2 in the blood

The curve clearly shows that "directly proportional" is wrong. Directly proportional means linear which is not the case. At best in some narrow ranges that would be a very good approximation.

in the lecture, it's said that Hb has an increasing affinity to O2 the more O2 is bound to it

Is it a general statement, or does it relate only to the initial part, with the low partial pressures?

 

[samy4408]

The curve clearly shows that "directly proportional" is wrong. Directly proportional means linear which is not the case. At best in some narrow ranges that would be a very good approximation.
Is it a general statement, or does it relate only to the initial part, with the low partial pressures?

it is said as a general statement, it seems true before the inflection point but after, not. and that is the point.

 

[BillTre]

The hemoglobin protein as 4 oxygen binding sites. They are not independent. Due to the way to protein conformation changes as it binds oxygen, binding the second, third, and four oxygen molecules is "easier".
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3699289/

This is considered a classic example of cooperative binding.

 

[samy4408]

The hemoglobin protein as 44 oxygen binding sites. They are no independent. Due to the way to protein conformation changes as it binds oxygen, binding the second, third, and four oxygen molecules is "easier".
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3699289/

This is considered a classic example of cooperative binding.

thank you very much for your reply, it's just that when I heard " the more oxygen is bound to hemoglobin, the easier it is for more oxygen to bind" i thought directly to an exponential curve, in reality, a sigmoid curve resembles an exponential curve in the beginning until saturation (the factor that I missed ) plays a role to reduce the slope.

 

[epenguin]

It gets easier to bind when some oxygen is already bound but on the other hand there are fewer empty sites to bind to, making binding more difficult if we speak loosely.

So let's not speak loosely, let's speak physically, thermodynamically – the only physically meaningful measure of "ease of binding" is an equilibrium constant:

K = [unoccupied sites][oxygen concentration]/[unoccupied sites] often written
$$ K = \frac {X}{x(1 - X)}$$
where $X$ is the saturation (= fraction of sites occupied by oxygen or other ligand, $x$ is the ligand solution concentration.) The above expression is an equilibrium constant, K is an association constant - which, er, varies as a function of saturation if you have cooperativity.

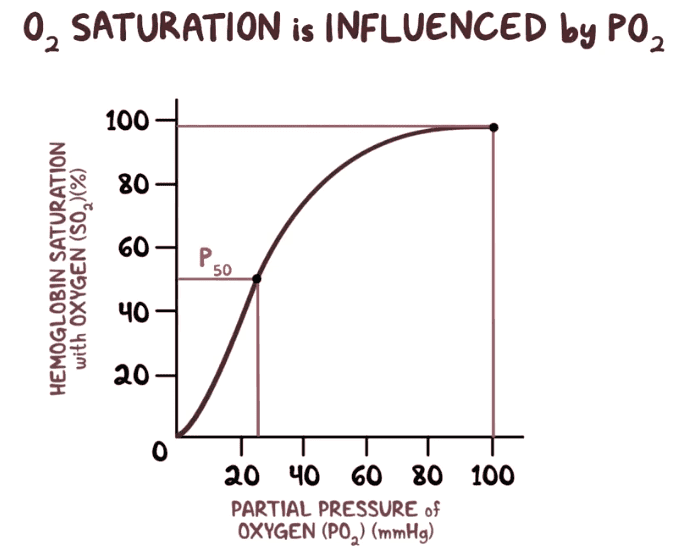
If I were teaching the subject I would not mention the word sigmoid at all, except as warning. It leads to confusion and even wrong statements sometimes, but the term is very frequently used in introductions to the subject.

Actually binding data is not so often reported as saturation saturation against ligand solution concentration (or equivalent lead here as gas pressure which ideally is proportional to solution concentration*); rather it is reported in the "Hill Plot" as
$log \frac{ X}{1-X}$ against $log x$
If there is no cooperativity the slope of the plot is exactly 1, where there is positive cooperativity it is higher.

You might find helpful to to consider a family of non-cooperative learning curves binding curves. Obeying, that is, the equation
$$ X = \frac {x}{K + x}$$
The lower K, the lower the ligand concentration needed to fill the binding sites. If you look at an individual curve you might naïvely say binding gets more difficult in each of them the more that is already bound. But from our definition of difficulty, they have the same equilibrium binding constant at all points along a given curve. On the other hand a cooperative curve (red) if it has a point in common with one noncooperative curve (blue), its next - higher concentration - points will intersect other curves corresponding to higher affinity.