Ulnarian
- 27
- 0
So I've been trying to wrap my head around the concept of the direction of current flow. I thought a voltage divider would be a good place to start. One website I've visited told me that the following image is a voltage divider. Both R1 and R2 will work together to affect the voltage of V(out).
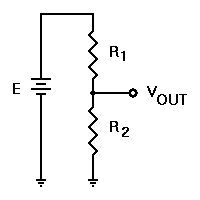
What I can't figure out is how R2 can possibly have an effect on V(out). Doesn't R2 appear in the circuit after the V(out) branch. Wouldn't the voltage going to V(out) just be whatever is remaining after it is reduced by R1? Or, does the current travel through R1, down to R2, and then back up to V(out)? Or something else?
Thanks!
What I can't figure out is how R2 can possibly have an effect on V(out). Doesn't R2 appear in the circuit after the V(out) branch. Wouldn't the voltage going to V(out) just be whatever is remaining after it is reduced by R1? Or, does the current travel through R1, down to R2, and then back up to V(out)? Or something else?
Thanks!