AC circuit - voltage drop and resonance

[Rugile]

Homework Statement

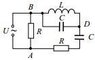
An AC voltmeter connected to the nodes A and B shows the same value as when connected to the nodes A and D (refer to attachment). What is the inductance of the inductor? What value does the voltmeter show? The inductor is ideal. U = 70sin(314t) V, C = 80 μF, R = 500 Ω.

Homework Equations

U_{rms} = \frac{U_{max}}{\sqrt{2}}
Z_L = i \omega L; Z_C = -\frac{i}{\omega C}
\omega = \frac{1}{\sqrt{LC}}

The Attempt at a Solution

For the voltages to be equal, the voltage drop across the inductor and capacitor in parallel should be 0. I know that in the case of series resonance, the voltage drop across the inductor and the capacitor is 0. Although here we also have a capacitor in parallel of the inductor, and due to the parallel resonance the voltage across these two elements is maximum (infinite). So what is confusing me, is that what is the actual voltage drop when we have simultaneous resonances? Could we say that the across the capacitor in series it is -∞ V, across the inductor ∞ V, thus resulting in 0 V in total (in series)?

 

[ehild]

The voltmeter reads the rms value of the voltage. If the readings are the same it means the rms values of the voltages are the same. The phases can be different.

In case L=0 the voltages U_AB and U_AD are the same. But that is not the only possibility.


ehild

 

[NascentOxygen]

An AC voltmeter connected to the nodes A and B shows the same value as when connected to the nodes A and D

So what does this tell you about the voltage between B and D? How could you explain the occurrence of this value of voltage between B and D? What are its implications for the rest of the circuit?

 

[ehild]

So what does this tell you about the voltage between B and D? How could you explain the occurrence of this value of voltage between B and D? What are its implications for the rest of the circuit?

@NascentOxygen: Are you really suggesting that the voltage is zero between B and D?

ehild

 

[NascentOxygen]

@NascentOxygen: Are you really suggesting that the voltage is zero between B and D?

ehild

Shhhhhh! Not so loud! It was a hint directed to Rugile, it's his homework task.[/color]

 

[gneill]

I think the intent of the problem would be to find the non-trivial solution, or perhaps both the trivial and non-trivial solutions

 

[ehild]

Shhhhhh! Not so loud! It was a hint directed to Rugile, it's his homework task.[/color]

What you suggested was the first idea of the OP :

The Attempt at a Solution

For the voltages to be equal, the voltage drop across the inductor and capacitor in parallel should be 0.

which is wrong. If UBD is zero, UAB=UAD, but from the fact that the voltmeter measures equal voltages between A , B and A , D does not follow that UBD=0. Can you imagine something else, not so trivial?

ehild

 

[Rugile]

Thank you for all the answers!

So it does in fact have nothing to do with the resonance?

Why is the voltage the same when L = 0? Is it because of the phase shift?

This is really confusing! I don't really see any other way than UBD being zero. It seems pretty reasonable to me!

 

[ehild]

Thank you for all the answers!

So it does in fact have nothing to do with the resonance?

It is not connected to resonance.

Why is the voltage the same when L = 0? Is it because of the phase shift?

If L=0 the impedance of the inductor is zero. Connected parallel with C, the resultant is also zero. You can replace the parallel connected inductor and capacitor by a single wire of zero resistance connecting the points B and D. . There is no voltage drop across it, so the potential is the same at both points. This is the trivial solution of the problem.

This is really confusing! I don't really see any other way than UBD being zero. It seems pretty reasonable to me!

The impedances are complex quantities and so are the voltages.

The complex impedance of the parallel LC is Z_LC and that of the series R, C is Z_RC, $U_{AD}=U_{AB}\frac{Z_{RC}}{Z_{LC}+Z_{RC}}$

U_AD is not in phase with U_AB, but the voltmeter reads only the rms values. The two readings are equal - it means that the rms value (or the amplitude) of U_AD is equal to those of U_AB.
If $|U_{AD}|=|U_{AB}|$

$|\frac{Z_{RC}}{Z_{LC}+Z_{RC}}|=1$ follows.

Find L which satisfies the condition above.

ehild

 

[Rugile]

... true.

Isn't so bad afterall.

Thank you a lot!

 

[ehild]

Could you figure out L?

ehild

 

[Rugile]

Ok, so we get Z_{RC} = Z_{RC} + Z_{LC}, right?
Then Z_{LC} = 0 = \frac{-i \omega L * \frac{i}{\omega C}}{i \omega L - \frac{i}{\omega C}} = \frac{i \omega L}{1 - \omega^2 LC} and, well, the answer - L=0...

 

[ehild]

That is the trivial case. But the voltage readings are the same if the magnitude of Z_RC is equal to the magnitude of Z_RC+Z_LC, that is

$\big|R-\frac{j}{ωC} \big|=\big|R-\frac{j}{ωC}+\frac{jωL}{1-ω^2LC}\big|$

ehild

 

[Rugile]

Okay, so Zlc = -2Zrc ( if we say that Zlc is negative and the modulus of difference of Zrc and Zlc has to be equal to Zrc, Zlc has to be twice as big). Then after rearranging we get: L=\frac{2(i-R\omega C)}{3i \omega^2 C}. What do we do with the i? Should it be rearranged to L=a + ib, and L =√(a^2 + b^2)?

 

[NascentOxygen]

Thank you for all the answers!

So it does in fact have nothing to do with the resonance?

You included the word "resonance" in the thread's subject---is this question from the the resonance topic of your textbook?

Does the textbook give you the answer to this question?

http://imageshack.com/a/img440/6184/icon2p.gif Could you check back with the original question, and confirm that it states voltages AB and AD measure as the same value.

* If the question is as you say, then my earlier hints can be ignored, because I had inadvertently swapped A and B. Such a swap is logical for a question dealing with resonance, IMO.

 

[Rugile]

The problem is not from a textbook - I don't have the answer (I didn't make it up myself, either ) - and it's under a more broad topic - electromagnetism. I just though that resonance is probably the key to the problem.

And yes, the problem statement is correct in the first post.

 

[ehild]

Okay, so Zlc = -2Zrc ( if we say that Zlc is negative and the modulus of difference of Zrc and Zlc has to be equal to Zrc, Zlc has to be twice as big). Then after rearranging we get: L=\frac{2(i-R\omega C)}{3i \omega^2 C}. What do we do with the i? Should it be rearranged to L=a + ib, and L =√(a^2 + b^2)?

NO, L is real.

The impedances are complex quantities, Z=a+ib, and you get the magnitude (modulus) or absolute value of the impedance as $|Z|=\sqrt{a^2+b^2}$

Z_LC is imaginary, Z_RC is complex.

Collect the real and imaginary terms on the right side and take the magnitude in both sides of the equation

$\big|R-\frac{j}{ωC} \big|=\big|R-\frac{j}{ωC}+\frac{jωL}{1-ω^2LC}\big|$

ehild

Spoiler

Calculate what would an AC voltmeter measure between A and D if ωL=2/3 (1/(ωC))

 

[NascentOxygen]

I haven't looked at the maths, but from the circuit I anticipate there to be 3 correct answers, one of which is L=0.

 

[Rugile]

Collect the real and imaginary terms on the right side and take the magnitude in both sides of the equation

Got it...

|R- j\frac{1}{\omega C}| = | R - j(\frac{-1}{\omega C} + \frac{\omega L}{1 - \omega^2 L C} | => \sqrt{R^2 + (\frac{1}{\omega C})^2 } = \sqrt{ R^2 + ( \frac{\omega L}{1 - \omega^2 LC} - \frac{1}{\omega C} )^2 }
## ##

 

[Rugile]

Accidentally posted the post above before finishing it, and for some reason can't edit it, so I'll finish here:

|R- j\frac{1}{\omega C}| = | R - j(\frac{-1}{\omega C} + \frac{\omega L}{1 - \omega^2 L C} | => \sqrt{R^2 + (\frac{1}{\omega C})^2 } = \sqrt{ R^2 + ( \frac{\omega L}{1 - \omega^2 LC} - \frac{1}{\omega C} )^2 }
$\frac{1}{\omega^2 C^2} = (\frac{\omega L}{1-\omega^2 LC} - \frac{1}{\omega C})^2$
$\frac{1}{\omega C} = \frac{\omega L}{1-\omega^2 LC} - \frac{1}{\omega C}$
$L = \frac{2}{3 \omega^2 C}$

Thank you for the help (and patience)!

I haven't looked at the maths, but from the circuit I anticipate there to be 3 correct answers, one of which is L=0.

So is there one more answer?

 

[ehild]

\frac{1}{\omega^2 C^2} =\left( \frac{\omega L}{1-\omega^2 LC} - \frac{1}{\omega C}\right)^2. has two roots: L=0 and L=2/3 1/(w^2C)

ehild