Voltage Output from AC Generators with More Loops

[Korisnik]

Hello, I don't understand how more loops in the AC generator create bigger voltage. I understand when we talk about magnetic flux how it happens (rate of change of surface that's penetrated by field lines), but there's also the explanation that says "if the magnetic field penetrates the paper, and if the conductor moves to the right, then the force will be upwards", now by force, since it's actually creating a voltage source, (the force acts on positive charges, and the current flows from + to -) is equivalent to conventional current direction.

So the picture is here: http://sciencecity.oupchina.com.hk/npaw/student/glossary/img/slip_rings.jpg
Now if you look at the loops you notice that if the loop that's farthest from the center of rotation actually moves like a tangent to a small circle, so it doesn't rotate, it goes in circles! Now if the loop were in the position that the holes were on the sides and the wires were up and down, then, looking from the north pole side, the lower part of the loop moves upwards, but SO DOES the upper part of the loop (because they aren't in the center of the rotation).

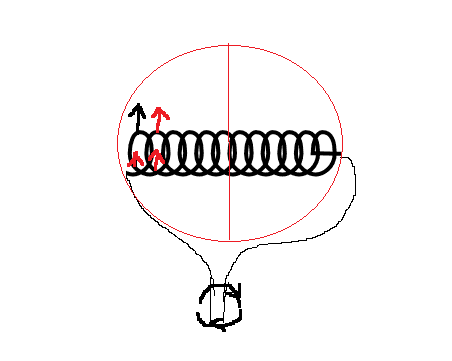
Since both upper and lower parts of the loop move upwards, by the left hand rule I described earlier the current goes in the same direction in upper and lower part of the wire; since the wire of the loop is continuous, the currents (voltages) should interact and annihilate one another. Why isn't this so?

 

[Simon Bridge]

It should help you to clear up your thinking if you concentrate on making a clearer description.

...you notice that if the loop that's farthest from the center of rotation

I see three loops in that diagram ... the center of each loop is on the axis of rotation. So all the loops are equally far from it.
Do you mean the biggest loop? That's just the way the diagram is drawn.

...actually moves like a tangent to a small circle...

... the loop rotates about an axis through it's center, it does not move on a tangent.
Do you mean that the part of the wire drawn close to the magnetic pole moves on a circular path?

doesn't rotate, it goes in circles!

... rotating is a form of going in circles. The upper diagram shows loops rotating about a common axis.

Now if the loop were in the position that the holes were on the sides and the wires were up and down, then, looking from the north pole side, the lower part of the loop moves upwards, but SO DOES the upper part of the loop (because they aren't in the center of the rotation)

The whole loop rotates. Every part of it.

Since both upper and lower parts of the loop move upwards, by the left hand rule I described earlier the current goes in the same direction in upper and lower part of the wire; since the wire of the loop is continuous, the currents (voltages) should interact and annihilate one another. Why isn't this so?

... you have misapplied the right hand rule.
The current should go in the same direction in every part of the wire.
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/genhow.html
... many loops just do the same thing as a single loop.

I don't see where the lower diagram comes in.

 

[Korisnik]

It should help you to clear up your thinking if you concentrate on making a clearer description.
I see three loops in that diagram ... the center of each loop is on the axis of rotation. So all the loops are equally far from it.
Do you mean the biggest loop? That's just the way the diagram is drawn.
... the loop rotates about an axis through it's center, it does not move on a tangent.
Do you mean that the part of the wire drawn close to the magnetic pole moves on a circular path?
... rotating is a form of going in circles. The upper diagram shows loops rotating about a common axis.

The whole loop rotates. Every part of it.
... you have misapplied the right hand rule.
The current should go in the same direction in every part of the wire.
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/genhow.html
... many loops just do the same thing as a single loop.

I don't see where the lower diagram comes in.

Maybe I wasn't clear on what my question was. It's, how is it possible, if you apply the left hand rule (we use the left hand rule that's the same as the rule you provided on that link) that the voltage is multiplied by the number of loops?

The lower diagram is the same as the upper picture but it's more clearer because the loops are smaller so you can clearly see that the loop that's the farthest from the center of the coil won't rotate around itself, but around the center of the rotation, which is in the middle of the coil. When you have only ONE loop, the rule is as it's shown on the link you've written here, and I'm using that same rule for when there are more loops, more turns. I draw arrows on the diagram that are velocity vectors, and it's clear that both parts of the loop (loop is an unconnected ring that has upper and lower half) upper and lower have the same velocity vector. So if you apply the left hand rule to this ring, they will have the induced voltage in the same direction. Since both parts of the loop are obviously connected, the current will have two directions, so there won't be any current. Which is different from the case when there's only ONE loop, when you again have 2 halves but since they go in different directions (have opposite velocity vectors), the voltage is induced in the opposite ways which means, because the wire is connected, the current will flow in that ONE loop. BUT here we have more loops!

When I said the farthest most loop doesn't rotate, I meant it doesn't rotate around itself, but around the axis that's in the middle of the coil; which is the main reason I cannot understand why there actually (experimentally) is current.

 

[sophiecentaur]

Think of it this way and only consider the sections of wire that are parallel to the axis of rotation: Every piece of wire that is moving upwards, is producing a small emf and all those emfs are in the same direction. All the pieces that are moving down are producing emfs in the other direction. So all those emfs are acting in the same sense around all those separate looks of wire and will add together around the (many) loops - giving a resulting total that is 2n times that of just one of the lengths of wire. This is like when you include more and more series batteries (connected the right way round) to get more volts. This total will alternate as the respective sides of the coil rotate through the field, going up and down through the field. The sinusoidal nature of the variation is because the speed that the coils cut through the field lines changes as the coils rotate (maximum when the motion is at right angles to the lines).

 

[jerromyjon]

I think you are confusing the two types of coils and superimposing them into one unit.

The upper picture shows 3 loops of straight wire (cyan with arrows depicting the flow of voltage) and the lower picture depicts a coil as in a solenoid where the charge/force would be left/right on the surface of the paper.

If you superimpose the coil onto the straight wire (cyan) then you are correct, no voltage would be created rotating the large coil of smaller coils.

 

[sophiecentaur]

I think you are confusing the two types of coils and superimposing them into one unit.

The upper picture shows 3 loops of straight wire (cyan with arrows depicting the flow of voltage) and the lower picture depicts a coil as in a solenoid where the charge/force would be left/right on the surface of the paper.

If you superimpose the coil onto the straight wire (cyan) then you are correct, no voltage would be created rotating the large coil of smaller coils.

I wasn't considering the hand drawn diagram because it is not 'optimal' (no one would ever design an alternator that looked like that). Nonetheless, you will still get a resulting emf from the emfs produced in the whole length of wire. Even for the loops that are traveling 'around' the axis, there will be a greater emf produced in the outer parts than for the inner parts (which would be in the opposite direction) and produce a no-zero net emf.

 

[jerromyjon]

I wasn't considering the hand drawn diagram because it is not 'optimal' (no one would ever design an alternator that looked like that).

I was trying to figure out something myself when the misconception of the OP struck me so I stated the simple error neglecting the implications.

Even for the loops that are traveling 'around' the axis, there will be a greater emf produced in the outer parts than for the inner parts (which would be in the opposite direction) and produce a no-zero net emf.

What I'm having trouble visualizing is the orientation of the magnetic field lines as in the first image, which I'm pretty sure is a DC generator.

 

[sophiecentaur]

I was trying to figure out something myself when the misconception of the OP struck me so I stated the simple error neglecting the implications.

What I'm having trouble visualizing is the orientation of the magnetic field lines as in the first image, which I'm pretty sure is a DC generator.

I agree that the first paragraphs of the OP are a bit muddled and the two diagrams are significantly different. Applying the LHRule to the wires in the first diagram, the only emfs generated are all in phase. In the second one, some of the emfs are induced in the 'wrong' direction. Nevertheless, there will be a net emf that is non zero and alternates.

No; it is a very basic alternator. To generate DC, there would need to be a commutator instead of the simple slip rings and brushes. As the coil rotates through a full 360 degrees, both polarities of emf are produced at the output terminals.

 

[jerromyjon]

This is what has always confused me and I'm trying to get it straight. What determines the direction of voltage at any given position in the rotation?

 

[Korisnik]

Think of it this way and only consider the sections of wire that are parallel to the axis of rotation: Every piece of wire that is moving upwards, is producing a small emf and all those emfs are in the same direction. All the pieces that are moving down are producing emfs in the other direction. So all those emfs are acting in the same sense around all those separate looks of wire and will add together around the (many) loops - giving a resulting total that is 2n times that of just one of the lengths of wire. This is like when you include more and more series batteries (connected the right way round) to get more volts. This total will alternate as the respective sides of the coil rotate through the field, going up and down through the field. The sinusoidal nature of the variation is because the speed that the coils cut through the field lines changes as the coils rotate (maximum when the motion is at right angles to the lines).

I understand all of that, but you imply that there are always a velocity vector of the conductor and the other one (that's parallel to the rotation axis) in the OPPOSITE direction on the SAME LOOP. What I wanted to show with the diagram below is that if you add more of these loops, then straighten the wires, you will have both upper and lower wire moving UPWARDS, (velocity vector is upwards) which means that the voltages are going to interact and destroy each other UNTIL the upper wire reaches the top...

 

[Korisnik]

This is what has always confused me and I'm trying to get it straight. What determines the direction of voltage at any given position in the rotation?

Try to apply left hand rule, the direction of the force determines the + pole of the induced voltage. If the (first picture) conductor is moving upwards, and we are looking at it from N-pole, the force will act on "positive charges" to the left, and by Newton's 3rd law the electric force will push negative charges to the right. Also the other wire (lower) moves downwards, so the same rule applies and the 2 voltages superposition. (The magnetic field lines go from N to S pole.)

If you superimpose the coil onto the straight wire (cyan) then you are correct, no voltage would be created rotating the large coil of smaller coils.

I never said something like that. I want to just give more loops to the first picture and make it clearer. The arrows represent the velocity vectors of the conducing wires that SHOULD BE parallel to the axis of rotation (but in case of coil, they aren't). Applying left hand rule to this case, and the voltage created should annihilate because the vectors can be of the same direction on the same loop.

 

[jerromyjon]

I still don't get it... and the terminology being used is adding confusion. Can we simplify this down to one wire moving across one pole of a magnet?

Let's say we have a north pole of a magnet on the left of the screen and a single loop of wire in the shape of "D" to the right. If I were to move the D from out here in my room through the screen, passing close to the north pole of the magnet with the vertical straight line, would the voltage flow up or down?

 

[sophiecentaur]

I still don't get it... and the terminology being used is adding confusion. Can we simplify this down to one wire moving across one pole of a magnet?

Let's say we have a north pole of a magnet on the left of the screen and a single loop of wire in the shape of "D" to the right. If I were to move the D from out here in my room through the screen, passing close to the north pole of the magnet with the vertical straight line, would the voltage flow up or down?

That's not a good idea, am afraid because the field around a pole, well away from another pole is almost radial so the direction is not defined. To simplify things you need a straight wire moving through a uniform field - say across a small gap between two large, parallel, flat poles. The induced emf is then proportional to vXB (the vector cross product of the velocity and the Field - which includes the LH Rule as a special case). If you can get to grips with what that means then the arm waving is not needed and you can get the right answer in all circumstances. Refusing to use the Maths makes life so much harder (and not easier).

You wrote: "I understand all of that"

With respect, I don't think you can do if you don't see what the result is. If two parallel wires are moving through a field with different velocities (at any positions relative to the axis of rotation will do) there will be a different emf induced in them so there will be a net non-zero emf - the maximum being when they are diametrically opposite. If they are rotating around an axel. the velocities will always be different if they are not in the same place.

PS talking in terms of moving charges is not actually necessary at this stage. Start off with a simple current.

 

[Korisnik]

You wrote: "I understand all of that"

With respect, I don't think you can do if you don't see what the result is. If two parallel wires are moving through a field with different velocities (at any positions relative to the axis of rotation will do) there will be a different emf induced in them so there will be a net non-zero emf - the maximum being when they are diametrically opposite. If they are rotating around an axel. the velocities will always be different if they are not in the same place.

Talking about a armature that consists of several loops but we are looking at the loop that's farthest away from the center.
If both wires are parallel and are parallel to the poles and are for example near the north pole. If the whole loop is moving upwards, at that moment both upper and lower wire are moving upwards meaning voltage is induced, but yes, since upper wire's velocity vector is almost near the top (near 0 angle with , meaning no voltage, the lower wire will provide voltage that will overcome the small one from upper wire. So net voltage will exist.

 

[sophiecentaur]

Talking about a armature that consists of several loops but we are looking at the loop that's farthest away from the center.
If both wires are parallel and are parallel to the poles and are for example near the north pole. If the whole loop is moving upwards, at that moment both upper and lower wire are moving upwards meaning voltage is induced, but yes, since upper wire's velocity vector is almost near the top (near 0 angle with , meaning no voltage, the lower wire will provide voltage that will overcome the small one from upper wire. So net voltage will exist.

We're talking about motion around an axle. If they are at different radii or at different angles (anything but absolutely co-incident) then they are not going at the same velocity. Hence, there will be a difference in the induced emfs. (Except, of course when the motion of both is parallel to the field lines; that's a zero crossing of the AC)

 

[sophiecentaur]

Re-reading what you have written, I am not sure what you are trying to say. Do you agree or disagree with what I have written?

 

[jerromyjon]

I'm still having trouble visualizing the orientation of the field lines...

 

[Korisnik]

Re-reading what you have written, I am not sure what you are trying to say. Do you agree or disagree with what I have written?

I agree, I realized that the voltage of the upper wire will (till it reaches he top) be smaller (and will tend to 0 as the angle between velocity vector and magnetic field vector approaches 0) so the lower wire's voltage will prevail and net voltage will exist.

 

[Korisnik]

I'm still having trouble visualizing the orientation of the field lines...

Field goes from N to S so you need 2 magnets. You place the wire between these magnets but perpendicular to the line in which the magnets are. Then move the wire upwards, + potential creates at left and - at right watching from the north pole.

 

[jerromyjon]

The voltage potential is between the entire loop of wire from the N to S poles of the field. Why does the + happen on the left and not the right?

 

[Korisnik]

Imagine magnets being in one line and wire horizontal but perpendicular to that line. Then the magnetic field acts on that wire from N to S. Now you are looking from the N to the S pole. Then if you move the wire upwards, the force acts on positive charges on the left and negative move to the right. So this wire is a voltage source. Thats just a straight wire not loop. If you have a loop you have to rotate it. You rotate one part up and other part down. The same rule applies so voltage is in one direction in he upper part of the loop and in the other in down part of the loop (because it moves downwards). Since its a wire, and is bent, when you would straighten it but leave the effect of the field and everything as if it were the loop, you would have a straight wire with double voltage that superpositions.

Also why exactly + on right is according to the law, formula, principle. Its + because it pushes + charge in he direction of the force. If there were - charges they would be pushed to the left.

 

[sophiecentaur]

The voltage potential is between the entire loop of wire from the N to S poles of the field. Why does the + happen on the left and not the right?

The rules of induction 'happen' at every position. The voltage potential is between the ends of the wires - not the 'poles'.
I assume you have looked at the Wiki article on simple alternators; it shows the field lines and the motion of a single (usual) rotating coil. That is the basis of the rest of the content of this thread. It is easier to assume the coils are rectangular so that you can ignore the radial bits of wire (they do not cut any field lines). If you understand that all of the wires in your multiple coil will have some emf induced and that the emfs are all different (some will be zero at times) - depending upon where they lie in the field and their speed (i.e. the velocity) at any time. When you connect them all in series (that is by the radial portions of all the coils - contributing nothing) the volts at the output will just be the sum of all these emfs. The resulting waveform will be symmetrical about zero - the details of the actual shape will depend on how the wires are actually laid out - I do not think you could expect the output to be necessarily sinusoidal but could contain harmonics of the rotation frequency.

Are there any more questions you could possibly ask?? ;)

 

[jerromyjon]

What determines which direction the electricity flows?

 

[jerromyjon]

I have always been under the impression it is path of least resistance, so if I remove the top bulb it lights up that LED which has an affinity for illuminating in that direction of drift velocity current otherwise the circuits need to be "balanced" along those paths and allowed to gyrate naturally.

Anyone see what I'm getting at? Does this post copyright it?

 

[sophiecentaur]

View attachment 75279
What determines which direction the electricity flows?

The sign of the result of the cross product - what else?
And how would one of those bulbs be on when the other is off? what about Kirchoff's Laws? This gets more outrageous with every post.

 

[Simon Bridge]

Field goes from N to S so you need 2 magnets. You place the wire between these magnets but perpendicular to the line in which the magnets are. Then move the wire upwards, + potential creates at left and - at right watching from the north pole.

... I think I see what you are trying to describe: you have just one long straight wire that you move through the field of two magnets... one of the magnets is reversed wrt the other one so part of the wire moves past a north pole and part moves past a south pole. This right?

This situation is not equivalent to the generator diagram.

 

[sophiecentaur]

I really can't decide what the OP's motives for this thread are. He wants an explanation why a strange arrangement of coils will still produce a non zero AC output when rotated. That explanation has been given - pretty thoroughly - using a simple model (which is always the best way through an explanation. So now he is shifting the goal posts but to what end?

 

[jerromyjon]

I'm thinking of something totally different from an alternator, and I'm not the OP.