Raghav Agarwal
- 11
- 0
Homework Statement
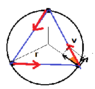
Three particles A, B, C, are situated at the vertices of equilateral triangle of side l. They approach each other with velocity v, such that A always moves toward B, B towards C and C towards A. What will be the initial acceleration?
Homework Equations
The Attempt at a Solution
Using vector components, I have found the acceleration
a=vapproach*(rate of change of direction of velocoty vector
a=(3v/2)*(dθ/dt)
However I could not calculate this rate. I have tried to form trigonometric relations and differentiate them but it failed, and I am out of any new ideas.
Last edited by a moderator: