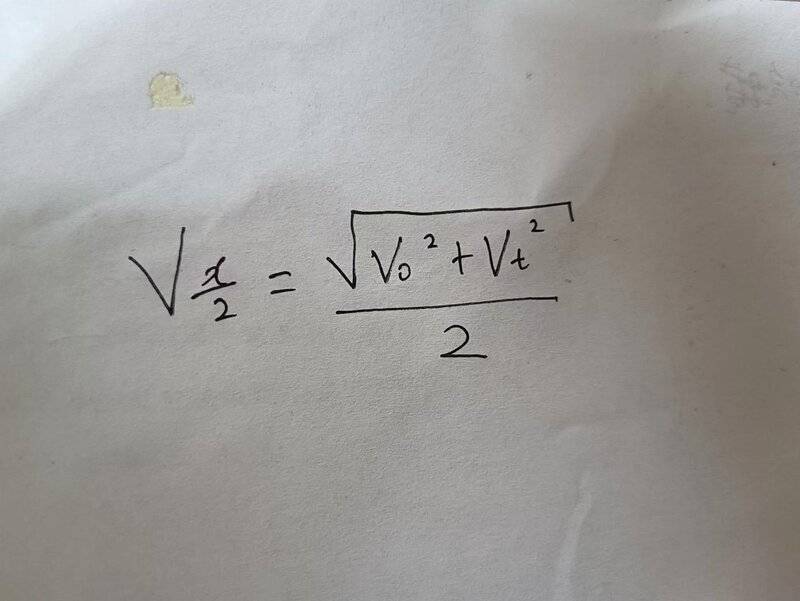B Acceleration -- How is the intermediate displacement speed derived?

[huc369]

TL;DR Summary

How is the intermediate displacement speed derived?

I don't know if I wrote it correctly

 

[PeroK]

Do you know any SUVAT equations?

 

[huc369]

SUVAT

Thank you very much, I will google it

 

[vanhees71]

How do you know that the "SUVAT Equations" apply? I don't understand, which problem is to be solved to begin with. Without asking a clear question, you can't get anything done in science!

 

[robphy]

Summary: How is the intermediate displacement speed derived?

I don't know if I wrote it correctlyView attachment 315157

Since SUVAT involves constant-acceleration,
and constant-velocity (zero acceleration) is a special case,
consider your proposed formula in the zero-acceleration case, where $v_0=v_B=v_T$
(where B represents the intermediate displacement: $(x_B-x_0)=\frac{1}{2}(x_T-x_0)$ in your time interval $0\leq t\leq T$).

Assume $v_B>0$.
Your proposed formula would read
$$v_B=\frac{\sqrt{(v_B)^2+(v_B)^2}}{2}=\frac{v_B}{\sqrt{2}}\qquad\mbox(false).$$
Instead, it should (based on the symbols available in your recollection) be
$$v_B=\sqrt{ \frac{(v_0)^2+(v_T)^2}{2}}$$
so that $$v_B=\sqrt{ \frac{(v_B)^2+(v_B)^2}{2}}=v_B.$$
(Technically, to be a speed, the left-hand side should be $|v_B|$.)

Now, following @PeroK 's suggestion to your question,
this could be derived using SUVAT (the constant acceleration equations).