Acceleration of a point on square

[Tanya Sharma]

Homework Statement

2. Homework Equations [/B]

The Attempt at a Solution

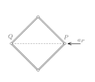
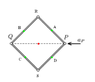
The origin is placed to the right of point P and left is taken to be the positive direction.Let us call mass of each rod as M and the angle which rods make with the horizontal as θ .

Coordinates of A = ($x_P+\frac{L}{2}cosθ,\frac{L}{2}sinθ$ )

Coordinates of B = ($x_P+\frac{3L}{2}cosθ,\frac{L}{2}sinθ$ )

Coordinates of C = ($x_P+\frac{3L}{2}cosθ,-\frac{L}{2}sinθ$)

Coordinates of D = ($x_P+\frac{L}{2}cosθ,-\frac{L}{2}sinθ$ )Now writing some constraint equations ,

$x_q = x_p + 2Lcosθ$

$v_q = v_p -2L(sinθ\dot{θ})$

$a_q = a_p -2L(cosθ\dot{θ}^2+sinθ\ddot{θ})$

$a_{cm} = \frac{1}{2}(a_p+a_q)$

The force applied on the square F= 4Ma_cm . This force produces displacement of P ,x_P in a very short time interval 't' . $x_P = \frac{1}{2}a_Pt^2$

Work done on the square =Fx_P .

Now we will calculate the velocities of the CM of the rods .

$v_{A,x} = v_{P,x} - \frac{L}{2}sinθ\dot{θ}$
$v_{A,y} = \frac{L}{2}cosθ\dot{θ}$
$v_{B,x} = v_{P,x} - \frac{3L}{2}sinθ\dot{θ}$
$v_{B,y} = \frac{L}{2}cosθ\dot{θ}$

Similarly we can write speeds of the two bottom rods .

Magnitude of vertical component of velocity of CM of all four rods would be equal . Magnitude of horizontal component of velocity of CM of two right side rods would be equal whereas that of two left side rods would be equal.Angular speeds of all four rods would be same .

Now applying Work Energy theorem ,

$$4M\frac{1}{2}(a_p+a_q)(x_P) = 2(\frac{1}{2}M){(v_{P,x}- \frac{L}{2}sinθ\dot{θ})}^2+2(\frac{1}{2}M){(v_{P,x}- \frac{3L}{2}sinθ\dot{θ})}^2 + 4(\frac{1}{2}M){(\frac{L}{2}cosθ\dot{θ})}^2 + 4\frac{1}{2}(\frac{ML^2}{12})\dot{θ}^2$$

In the above expression we can put $x_P = \frac{1}{2}a_Pt^2$ , $\dot{θ} = \ddot{θ}t$ and $v_{P,x} = a_Pt$.

$$4M\frac{1}{4}(a_p+a_q)(a_Pt^2) = 2(\frac{1}{2}M){(a_Pt- \frac{L}{2}sinθ(\ddot{θ}t))}^2+2(\frac{1}{2}M){(a_Pt- \frac{3L}{2}sinθ(\ddot{θ}t))}^2 + 4(\frac{1}{2}M){(\frac{L}{2}cosθ(\ddot{θ}t))}^2 + 4\frac{1}{2}(\frac{ML^2}{12})(\ddot{θ}t)^2$$

Is it correct till here ? If yes, how do I eliminate $\ddot{θ}$ ?

I would be grateful if someone could help me with the problem .

 

[ehild]

a_q can be also expressed by $\ddot \theta$. Solve for $\ddot \theta$, and determine a_q with it.

 

[Tanya Sharma]

Is there another expression between a_q and $\ddot \theta$ besides $a_q = a_p -2L(cosθ\dot{θ}^2+sinθ\ddot{θ})$ which I mentioned in the OP?

 

[ehild]

Is there another expression between a_q and $\ddot \theta$ besides $a_q = a_p -2L(cosθ\dot{θ}^2+sinθ\ddot{θ})$ which I mentioned in the OP?

It is enough.
The velocity terms vanish. You can substitute sinθ and cosθ with their valus at t=0.

 

[Tanya Sharma]

Thank you very much .