You should show your work in more details. You got 40 in what units? between which initial and final points? Shows us how you got this. As you can see, people are not interested otherwise in your problem, and loose themselves in a different conversation.
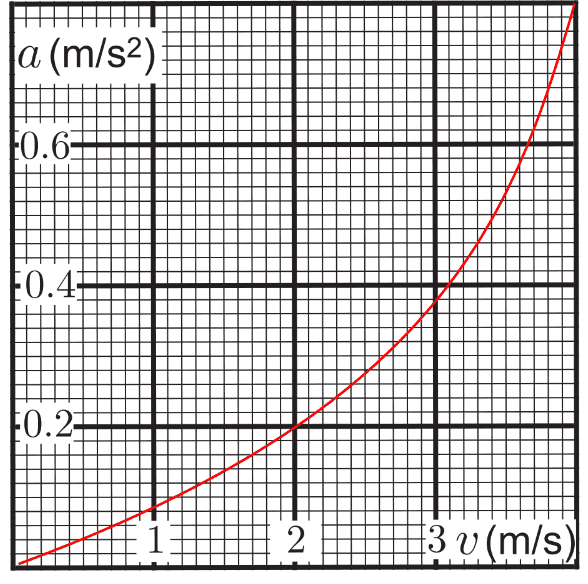
Assuming that the area under the curve is the distance traveled works only with a velocity vs time graph because ##\Delta x = v \Delta t## where an imaginary rectangle of height ##v## and width ##\Delta t## gives an area ##\Delta x##. This is not the case here.
@phyzguy basically did what I wanted you to do on your own in
post #9. When I told you to assume the acceleration is constant, it was an easy example for you to find out what final equation you would get, to better understand how it works. Obviously, the acceleration is
not constant in your case, it is a function of velocity.