mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
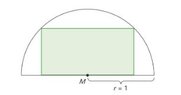
We have a rectangle inside a semicircle with radius $1$ :
View attachment 9703
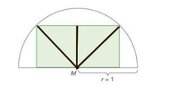
From the midpoint of the one side we draw a line to the opposite vertices and one line to the opposite edge.
View attachment 9704
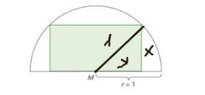
Are the acute angles of the right triangles all equal to $45^{\circ}$ ? (Wondering)
All four triangles are similar, aren't they? We have that the hypotenuse of each right triangle is equal to $1$, since it is equal to the radius of the circle.
I am stuck right now about the angles. (Wondering)
We have a rectangle inside a semicircle with radius $1$ :
View attachment 9703
From the midpoint of the one side we draw a line to the opposite vertices and one line to the opposite edge.
View attachment 9704
Are the acute angles of the right triangles all equal to $45^{\circ}$ ? (Wondering)
All four triangles are similar, aren't they? We have that the hypotenuse of each right triangle is equal to $1$, since it is equal to the radius of the circle.
I am stuck right now about the angles. (Wondering)