mrajkumar
- 11
- 0
Hi,
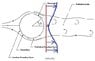
Could you explain the reason why the velocity varies in the wake region behind the cylinder in "flow over a circular cylinder"? the velocity variation is, minimum at a point parallel to the centre point of the cylinder and increases to free stream velocity as the vertical distance increases from the centre point. rough image file is added.
And is there a possibility that stagnation pressure varies in the wake region? Because my understanding is stagnation pressure should remain constant everywhere in the flow field. only static pressure varies in relation to dynamic pressure to maintain constant stagnation pressure.
Thank you
Could you explain the reason why the velocity varies in the wake region behind the cylinder in "flow over a circular cylinder"? the velocity variation is, minimum at a point parallel to the centre point of the cylinder and increases to free stream velocity as the vertical distance increases from the centre point. rough image file is added.
And is there a possibility that stagnation pressure varies in the wake region? Because my understanding is stagnation pressure should remain constant everywhere in the flow field. only static pressure varies in relation to dynamic pressure to maintain constant stagnation pressure.
Thank you